Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Линейные операторы, действующие в произвольном линейном пространстве

Глава 7 Линейные операторы

Линейным оператором , действующим в линейном пространстве над числовым полем (или линейным преобразованием линейного пространства над числовым полем ), называется правило, по которому каждому элементу из 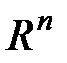ставится в соответствие определенный элемент из :

(71)

причем для любых элементов из 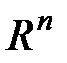и любого числа из поля выполняются равенства: 1° ;

2° .

Разложим элементы , , линейного пространства по базису : , 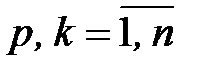(72)

Матрица называется матрицей оператора в базисе . Равенство (72) можно записать в матричной форме: , где - матрица-строка, составленная из базисных элементов 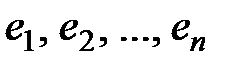и, следовательно, запись означает матрицу-строку . Соотношение (71) в координатах имеет вид , (73)

где , - матрицы-столбцы, составленные соответственно из координат элементов и в базисе , т.е. , .

При переходе от базиса к базису , осуществляемом по формуле , (74)

где 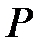- матрица перехода, столбцами которой являются , т.е. координаты элемента в базисе , матрица линейного оператора преобразуется в матрицу , (75)

причем . (76)

Операторы 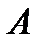и 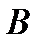называются равными, если .

Теорема 1 Если операторы равны, то в любом базисе равны и матрицы этих операторов.

Суммой линейных операторов и называется оператор такой, что .

Теорема 2 Если и - линейные операторы, то - линейный оператор.

Теорема 3 Матрица суммы операторов и в любом базисе равна сумме матриц операторов и 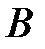в том же базисе, т.е. .

Произведением линейного оператора на число из , называется оператор такой, что .

Теорема 4 Если - линейный оператор, действующий в линейном пространстве над числовым полем , и число , то - линейный оператор.

Теорема 5 Матрица оператора в любом базисе равна матрице оператора в этом же базисе, умноженной на число , т.е. .

Теорема 6 Множество всех линейных операторов, действующих в линейном пространстве размерности над полем , с указанными операциями сложения и умножения на число из того же поля образует линейное пространство, причем .

Произведением линейных операторов и , действующих в линейном пространстве , называется оператор такой, что .

Теорема 7 Если и - линейные операторы, то - линейный оператор.

Теорема 8 Матрица оператора в любом базисе равна произведению матрицы оператора на матрицу оператора в том же базисе, т.е. .

Подпространство линейного пространства 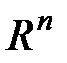называется инвариантным относительно линейного оператора , если для любого из элемент .

Пространства 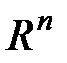и всегда являются инвариантными подпространствами для любого линейного оператора, действующего в .

Если линейное пространство определено над числовым полем , то число из поля называется собственным значением линейного оператора , если существует ненулевой элемент из 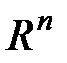такой, что

(77)

Элемент называют собственным вектором линейного оператора .

Уравнение (78)

называется характеристическим уравнением линейного оператора , действующего в линейном пространстве над числовым полем и имеющего в базисе матрицу . При этом многочлен от называется характеристическим многочленом оператора в базисе .

Теорема 9 Характеристический многочлен оператора не зависит от выбора базиса в линейном пространстве.

Если - решение уравнения (78), принадлежащее полю , то - собственное значение линейного оператора , а все множество решений системы линейных уравнений (79)

является множеством столбцов из координат тех элементов из , которые образуют инвариантное относительно линейного оператора подпространство , соответствующее данному собственному значению . Если из последнего подпространства удалить нулевой элемент, то оставшееся множество элементов есть множество всех собственных векторов линейного оператора , соответствующих собственному значению .

Базис в линейном пространстве 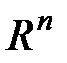, в котором действует линейный оператор , составленный из собственных векторов оператора (если такой базис существует), называется собственным базисом оператора .

Линейный оператор называется обратным к оператору , если .

Оператор, обратный к , обозначается символом .