
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. Привести к каноническому виду уравнение кривой, нарисовать кривую , и найти координаты центра в первоначальной системе координат.
|
|
Привести к каноническому виду уравнение кривой, нарисовать кривую 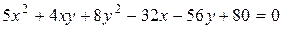 , и найти координаты центра в первоначальной системе координат.
, и найти координаты центра в первоначальной системе координат.
Решение.
Дано уравнение кривой в общем виде  .
.
Выведем формулы преобразования. Начнем с поворота осей. Целью этого преобразования, является уничтожение в преобразованном уравнении члена, содержащего произведение текущих координат.
Формулы преобразования координат поворотом осей без изменения начала координат имеют вид 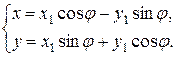
Подставляя эти значения 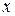 и
и 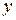 в заданное уравнение, будем иметь
в заданное уравнение, будем иметь
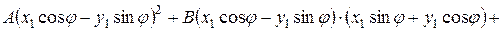
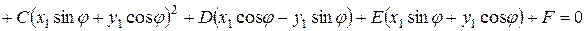 .
.
Раскроем скобки и получим

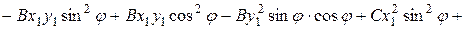

Сделаем приведение подобных членов:


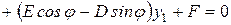 . (58)
. (58)
Выберем теперь угол поворота  так, чтобы коэффициент при
так, чтобы коэффициент при  обратился в нуль. Приравнивая этот коэффициент нулю, получаем уравнение для определения значения угла
обратился в нуль. Приравнивая этот коэффициент нулю, получаем уравнение для определения значения угла  , при котором этот коэффициент обратится в нуль:
, при котором этот коэффициент обратится в нуль:
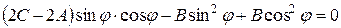 .
.
Разделим обе части этого уравнения на 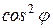 (
( , так как если
, так как если  , то
, то 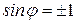 , и тогда это уравнение не имеет места, ибо получается, что
, и тогда это уравнение не имеет места, ибо получается, что  . Это замечание следует помнить и при решении последующих задач). После деления получим
. Это замечание следует помнить и при решении последующих задач). После деления получим
 ,
,
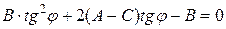 .
.
Решая квадратное уравнение получим два значения  и
и  .
.
Теперь перейдем к нашему примеру, учитывая 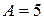 ,
,  ,
,  :
:
 . Отсюда получаем для тангенса угла
. Отсюда получаем для тангенса угла  поворота координатных осей такие значения:
поворота координатных осей такие значения: 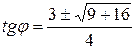 или
или  и
и  .
.
Эти два значения  соответствуют двум взаимно-перпендикулярным направлениям, так как произведение этих тангенсов равно
соответствуют двум взаимно-перпендикулярным направлениям, так как произведение этих тангенсов равно  . Из
. Из  следует, что угол поворота
следует, что угол поворота  может находиться в первой или третьей четвертях, а из
может находиться в первой или третьей четвертях, а из  следует, что угол поворота
следует, что угол поворота  может находиться во второй или четвертой четвертях. Условимся всегда брать для
может находиться во второй или четвертой четвертях. Условимся всегда брать для  из двух возможных значений – положительное, а угол поворота
из двух возможных значений – положительное, а угол поворота  - в первой четверти
- в первой четверти 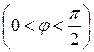 . Таким образом, из двух возможных значений тангенса берем
. Таким образом, из двух возможных значений тангенса берем  . Определим по известному
. Определим по известному  величину
величину 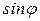 и
и  . Это нам нужно для того, чтобы определить коэффициенты при
. Это нам нужно для того, чтобы определить коэффициенты при 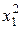 ,
, 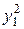 ,
,  и
и  в уравнении (58).
в уравнении (58).
Так как у нас  , а угол
, а угол  находится в первой четверти, то по известному
находится в первой четверти, то по известному  функции
функции 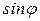 и
и  могут быть определены следующим образом:
могут быть определены следующим образом:  ,
,  . Из этого следует, что
. Из этого следует, что 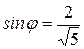 ,
, 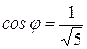 ,
, 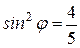 ,
, 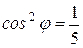 ,
,  . При найденных значениях
. При найденных значениях 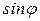 и
и  коэффициент при
коэффициент при 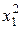 равен 9, коэффициент при
равен 9, коэффициент при  - нулю, коэффициент при
- нулю, коэффициент при 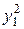 равен 4, коэффициент при
равен 4, коэффициент при  равен
равен  , а коэффициент при
, а коэффициент при  равен
равен  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Подставляя эти значения в уравнение (1), получим  .
.
Выделяя в скобках полные квадраты, имеем
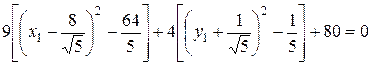 , откуда
, откуда 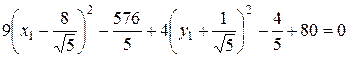 ,
,
или  . (59)
. (59)
 Введем обозначения:
Введем обозначения: 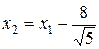 ;
; 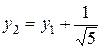 ;
;
из сравнения с формулами заключаем, что  ,
,  , а уравнение (59) перепишем так:
, а уравнение (59) перепишем так:  .
.
После деления обеих частей равенства на 36 получим Рисунок 95 данное уравнение в каноническом виде:  .
.
Итак, данное уравнение определяет эллипс. Он вытянут вдоль оси  .
.
Домашнее задание № 5/
1 Привести уравнение кривой к каноническому виду и нарисовать кривую:  .
.
Ответ. Кривая – гипербола, ее каноническое уравнение 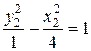
2 Привести уравнение кривой к каноническому виду  .
.
Ответ. Кривая – парабола, ее каноническое уравнение 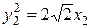
3 Привести уравнение кривой к каноническому виду  .
.
Ответ. Кривая – эллипс, его каноническое уравнение 
4 Построить кривую 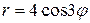 и найти ее уравнение в прямоугольных координатах при условии, что начало прямоугольных координат совпадает с полюсом полярной системы координат, а положительная полуось абсцисс совпадает с полярной осью.
и найти ее уравнение в прямоугольных координатах при условии, что начало прямоугольных координат совпадает с полюсом полярной системы координат, а положительная полуось абсцисс совпадает с полярной осью.
Ответ.  - трехлепестковая роза
- трехлепестковая роза
5 Построить спираль Архимеда 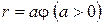 .
.
6 Построить кардиоиду 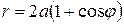
 .
.
7 Построить гиперболическую спираль 
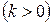 .
.
* Полярный угол измеряется в радианах.
|
|
