Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразование координат поворотом координатных осей без изменения начала координат
|
|
Если 
- угол поворота, 
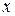и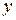 
- первоначальные координаты точки, 
и 
- координаты той же точки в новой, повернутой системе координат, то имеют место формулы
и 
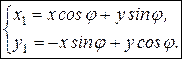(57)
Рисунок 93
Вопросы для самоконтроля
1 Сформулируйте определение эллипса. Запишите каноническое уравнение эллипса (изобразите эллипс).
2 Сформулируйте определение параболы. Запишите каноническое уравнение параболы (изобразите параболу).
3 Сформулируйте определение эксцентриситета эллипса, директрисы эллипса.
4 Сформулируйте определение эксцентриситета гиперболы, директрисы гиперболы.
5 Сформулируйте определение окружности. Запишите каноническое уравнение окружности.
6 Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис и асимптот гиперболы 
(изобразить гиперболу отметить фокусы и директрисы).
7 Сформулируйте определение гиперболы. Запишите каноническое уравнение гиперболы (изобразите гиперболу).
8 Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис эллипса 
(изобразить эллипс отметить фокусы и директрисы).
9 Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис эллипса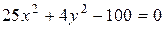 
(изобразить эллипс отметить фокусы и директрисы).
10 Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис и асимптот гиперболы 
(изобразить гиперболу отметить фокусы и директрисы).
11 Найти координаты фокуса, уравнения директрисы параболы 
(изобразить параболу отметить фокус и директрису).
12 Найти координаты фокуса, уравнения директрисы параболы 
(изобразить параболу отметить фокус и директрису).
13 Запишите уравнение линии 
в полярных координатах (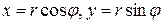
).
14 Привести уравнение кривой к каноническому виду и изобразить кривую, которая определяется уравнением: 
.
15 Запишите уравнение окружности с центром в точке 
и 
16 Дана точка 
, найти ее координаты в полярной системе координат.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
17 Запишите формулы перехода от полярной системы координат к декартовой и обратно.
18 Дана точка 
, найти ее координаты в декартовой системе координат.
19 Запишите формулы преобразования координат поворотом координатных осей без изменения начала координат
20 Запишите уравнение кривой в общем виде.
Практическое занятие № 5/
|
|