Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 1. Построить кривую и найти ее уравнение в прямоугольной системе координат.
|
|
Построить кривую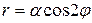 
и найти ее уравнение в прямоугольной системе координат.
Решение.
Будем давать значения полярному углу 
от 
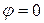до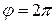 
через промежуток 
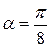и вычислим соответствующие значения 
. Найденные значения поместим в таблицу. Примем произвольный отрезок при построении . По значениям и из таблицы построим точки, соответствующие каждой паре чисел и , и соединим их плавной линией.
|
| 
| 
|
|
|
| |
| 
| 
| 
| |||
| 
|
| 
| 
| ||
|
| 
| 
| 
| 
| ||
| 
|
| 
| 
| 
| |
|
| 
|
| 
| 
|
| |
|
|
| 
| 
| ||
|
|
| 
| 
|
| ||
|
|
| 
| 
|
| |
|
|
|
|
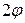
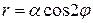
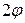
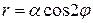
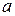
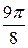
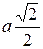
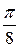
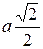
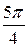
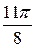
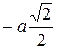
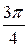
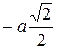
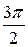
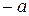
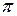
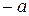
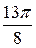
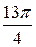
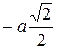
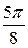
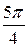
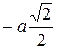
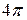
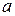
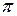
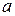
Полученная кривая называется четырехлепестковой розой.
Теперь найдем уравнение четырехлепестковой розы в прямоугольной системе координат. Причем напоминаем, что начало прямоугольной системы координат помещено в полюс полярной системы координат, а ось абсцисс направлена вдоль полярной оси.
Рисунок 94
Учитывая, что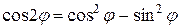 
, уравнение четырехлепестковой розы 
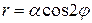перепишем в виде 
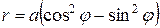. Подставляя сюда формулы перехода, получим
или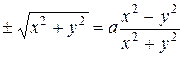 
.
Отсюда 
. Возводя обе части уравнения в квадрат, получим уравнение 
.
|
|