Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача 2. Доказать, что прямая , , параллельна плоскости .

Доказать, что прямая , , 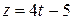параллельна плоскости .

Решение.

.

.

Прямая 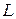параллельна плоскости , если направляющий вектор 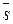прямой 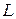перпендикулярен

Рисунок 59 нормальному вектору плоскости .

.

прямая параллельна плоскости.

Задача 3 Найти величину угла между прямой , , , и плоскостью .

Решение.

Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость.

.

Угол между прямой 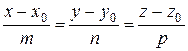и плоскостью : определяется по формуле

.

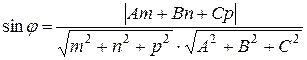Рисунок 60

.

.

, .

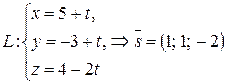Ответ.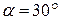

Задача 4 При каких значениях и прямая лежит в плоскости ?

Решение. Для прямой, которая задана каноническим уравнением

известен направляющий вектор и точка принадлежащая ей, с координатами . Для плоскости известен нормальный вектор .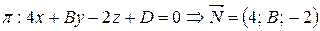

Прямая лежит в плоскости, если выполняются Рисунок 61 два условия: 1) и

2) точка лежит в плоскости , т.е.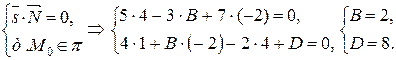

Ответ.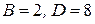

Задача 5 Установить взаимное расположение прямой и плоскости:

а) 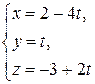и ;

б) и .

Решение.

а) Имеем, направляющий вектор прямой задан координатами , нормальный вектор плоскости задается координатами . Как видно координаты направляющего вектора 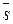прямой и нормального вектора плоскости не пропорциональны: прямая не перпендикулярна плоскости . Найдем значение выражения :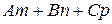

.

Условие параллельности прямой и плоскости не выполняется. Значит, прямая пересекает плоскость.

б) Здесь, вектора направляющий и нормальный заданы координатами и точка лежащая на прямой , , , проверим равенство . Следовательно, данная прямая параллельна плоскости или лежит на ней. Проверим условия принадлежности прямой плоскости: .

Условия выполняются, поэтому прямая лежит в плоскости.