Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Взаимное расположение прямой и плоскости в пространстве

Угол между прямо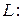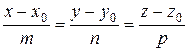й и

плоскостью определяется по формуле

. (35)

Рисунок 54

Условие параллельности прямой и плоскости в пространстве:

Прямая параллельна плоскости тогда и только тогда, когда направляющий вектор для прямой перпендикулярен нормальному вектору для плоскости, т.е.

; (36)

Рисунок 55

Условие перпендикулярности прямой и плоскости в пространстве:

Прямая перпендикулярна плоскости тогда и только тогда, когда направляющий вектор для прямой коллинеарен нормальному вектору для плоскости, т.е.

. (37)

Рисунок 56

Для нахождения точки пересечения прямой и плоскости удобно воспользоваться параметрическим уравнением прямой :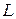

координаты точки пересечения находятся из системы уравнений

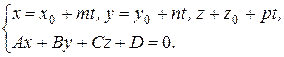(38)

Условие, при котором прямая 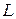лежит в плоскости

(39)

Рисунок 57

Если , то прямая пересекает плоскость; если и 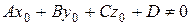- прямая параллельна плоскости.

Вопросы для самоконтроля

1 Запишите уравнение прямой 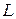в пространстве, проходящей через две различные точки и .

2 Запишите параметрическое уравнения прямой 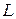в пространстве.

3 Сформулируйте признаки параллельности и перпендикулярности двух прямых в пространстве.

4 Сформулируйте условие, при котором две прямые 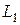и лежат в одной плоскости.

5 Запишите формулу нахождения угла меду прямыми в пространстве.

6 Запишите общее уравнение прямой в пространстве.

7 Запишите уравнение прямой 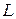, проходящей через данную точку 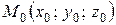параллельно вектору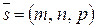

8 Выведите уравнение прямой 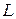в пространстве, являющейся пересечением двух плоскостей.

9 Составить уравнение прямой 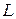, проходящей через точку М (1; 3; 0) и направляющий вектор

10 Укажите способы расположения прямой и плоскости в пространстве.

11 Уравнение прямой по точке и направляющему вектору.

12 Признак параллельности прямой и плоскости.

13 Взаимное расположение двух прямых в пространстве.

14 Признак перпендикулярности прямой и плоскости.

15 Признак принадлежности прямой к плоскости.

16 Угол между прямой и плоскостью в пространстве.

17 Параметрическое уравнение прямой в пространстве.

18 Каноническое уравнение прямой в пространстве.

19 Составить уравнение прямой 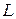, проходящей через точку М (1; 3; 0) и перпендикулярно плоскости

20 Составить уравнение прямой 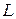, которая является пересечением двух плоскостей

и .