
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Различные виды уравнения прямой в пространстве
|
|
Глава 3 Прямая в пространстве
1 Каноническое уравнение прямой 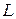 , проходящей через данную точку параллельно вектору
, проходящей через данную точку параллельно вектору 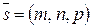
 (27)
(27)
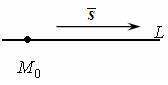
Рисунок 45
Вектор 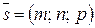 называют направляющим вектором для прямой
называют направляющим вектором для прямой 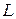 . Обращение в нуль одного из знаменателей уравнения (27) означает обращение в нуль соответствующего числителя.
. Обращение в нуль одного из знаменателей уравнения (27) означает обращение в нуль соответствующего числителя.
2 Параметрическое уравнение прямой 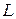 :
:  , (28)
, (28)
где 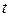 - переменный параметр,
- переменный параметр,  .
.
В векторной форме уравнение (28) имеет вид 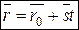 , где
, где  ,
,  .
.
3 Уравнение прямой, проходящей через две точки  и
и 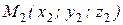 , где (
, где ( ,
, 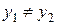 ,
, 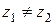 одновременно), имеет вид
одновременно), имеет вид

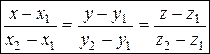 (29)
(29)
Рисунок 46
4 Общее уравнение прямой, которое задается пересечением двух плоскостей:
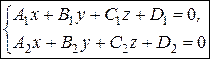
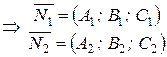
(коэффициенты при переменных не пропорциональны). Направляющий вектор прямой (27) находится по формуле
 или
или 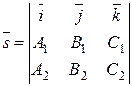 , т.е.
, т.е.  (30)
(30)
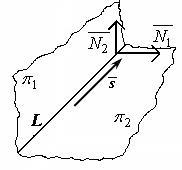
Рисунок 47
§2 Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых в пространстве. Условие компланарности двух прямых в пространстве
Пусть прямые 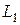 и
и  заданы уравнениями:
заданы уравнениями:
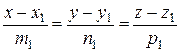 и
и  .
.
Под углом между прямыми понимают угол между их направляющими векторами 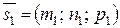 и
и  .
.
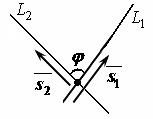
Рисунок 48
Для нахождения острого угла между прямыми 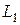 и
и  используют формулу вида:
используют формулу вида:
 (31)
(31)
Условие перпендикулярности двух прямых в пространстве:
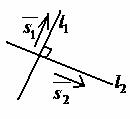 Две прямые в пространстве перпендикулярны тогда и только тогда, когда их направляющие вектора перпендикулярны, т.е.
Две прямые в пространстве перпендикулярны тогда и только тогда, когда их направляющие вектора перпендикулярны, т.е.

 (32)
(32)
Рисунок 49
Условие параллельности двух прямых в пространстве:
|
|
