Собственные колебания распределённых систем конечной длины

При исследовании колебательных процессов в распределённых системах конечной длины обычно используется метод Бернулли, т. е. решение разлагается по собственным функциям краевой задачи. Вид собственных функций существенно зависит от граничных условий, связывающих ток и напряжение или силу и смещение на границах системы.

Остановимся лишь на простейших случаях граничных условий, которые, однако, часто встречаются на практике.

Короткозамкнутому или разомкнутому концу соответствуют граничные условия вида

,   ,

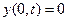(9.10)

где y - ток (для разомкнутой линии) или напряжение (для замкнутой линии).

Более общий случай граничных условий осуществляется в электрической линии, нагруженной на конце ёмкостью C ₀. Для напряжения на этой ёмкости и заряда справедливо следующее

.

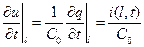Подставляя это соотношение в телеграфное уравнение (9.1), для линии без потерь получим:

.

Для конденсатора, включенного вначале линии в сечении x = 0, получаем

.

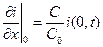Если на конце линии включена индуктивность L ₀, то граничные условия запишутся так:

,   .

Объединяя рассмотренные выше типы граничных условий, получим общий вид граничных условий такого рода

,   .

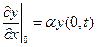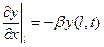(9.11)

Волновое уравнение (9.2) с граничными условиями вида (9.10) или (9.11) удобно решать методом разделения переменных (метод Бернулли). Положим y (x, t) = j (x) T (t), тогда общее решение имеет вид

Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer

Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.

Что умеет делать SeoHammer

— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.

SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.

Зарегистрироваться и Начать продвижение

.

(9.12)

Постоянные A_s и B_s определяются из начальных условий. Из решения (9.12) следует, что распределённые колебательные системы конечной длины имеют бесконечное множество собственных частот w_s, каждой из которых соответствует определённая форма колебаний j_s.

Для двухпроводной линии, подставляя разложение (9.12) в волновое уравнение (9.2), получим:

.

(9.13)

Общее решение уравнения (9.13) имеет вид

.

Если линия короткозамкнута на конце, то граничные условия вида (9.10) дают B = 0, w_sl / v = ps, т. е.

.

(9.14)

w_s = psv / l, s = 1, 2, … - набор эквидистантных собственных частот, j_s (x) - собственные функции. Легко показать, что собственные функции, отвечающие различным собственным частотам, ортогональны:

,   s ¹ q.

(9.15)

Отметим, что ортогональность собственных (нормальных) колебаний - общее свойство распределенных систем и систем с многими степенями свободы.

Если система с распределёнными параметрами неоднородна, например, в середину длинной линии включен конденсатор, то эквидистантность собствен­ных частот нарушается, и собственные функции уже не синусоидальные, но их ортогональность (9.15) сохраняется. Пример такой системы - лазер. Активная среда, внесённая в резонатор Фабри-Перо (систему с распределёнными пара­метрами), нарушает эквидистантность собственных частот резонатора. Поэтому генерируемые моды становятся не синхронизируемыми.