Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вынужденные колебания в системе с n степенями свободы

Для линейных систем справедлив принцип суперпозиции колебаний. Поэтому задача о вынужденных колебаниях в системе под действием любой периодической силы сводится к нахождению вынужденных движений системы в результате действия гармонической силы частоты w. Если рассматриваемая система консервативна, то уравнение её колебаний в матричной форме принимает вид:

.

(8.19)

Вынужденные колебания системы должны быть гармоникой той же частоты

,

(8.20)

где 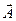- амплитудный вектор вынужденных колебаний. Подставляя решение (8.20) в (8.19), получим уравнение для амплитудного вектора

.

(8.21)

Таким образом, для отыскания выражения для вынужденного колебания в матричной форме необходимо обратить матрицу . Отметим, что в силу условия (8.5) в резонансе, т. е. при w = w_s, определитель этой матрицы равен нулю, следовательно, обратная матрица обращается в бесконечность.

Обращение матриц больших размеров - сложная задача, поэтому чаще используют другой метод - разлагают искомое решение по собственным колебаниям системы. Для этого амплитудный вектор 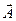разлагают по -векторам коэффициентов распределения амплитуды собственных колебаний системы:

.

(8.22)

Теперь задача сводится к отысканию неизвестных коэффициентов B_s. Внешнюю силу разложим следующим образом:

,

(8.23)

где f_s - коэффициенты разложения. Коэффициенты f_s можно найти, используя условие ортогональности (8.12). Умножая (8.23) слева скалярно на , запишем коэффициенты f_s в виде

.

(8.24)

Подставим теперь выражения (8.22) и (8.23) в уравнение (8.21), тогда

.

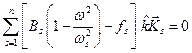(8.25)

Умножим уравнение (8.25) слева на , используя условие ортогональности нормальных колебаний вида (8.12), получим выражение для коэффициентов B_s:

.

Отсюда, с помощью формулы (8.22), находим амплитуды вынужденных колебаний:

.

(8.26)

Из формулы (8.26) видно, что при w ® w_s, амплитуда вынужденных колебаний всех координат стремится к бесконечности, т. е. происходит резонансное возрастание амплитуды. Резонанса на частоте w_s не будет, если вектор внешней силы ортогонален s -му нормальному колебанию, когда в соответствии с соотношением (8.24) получается f_s = 0.

При наличии затухания расчёт колебаний для систем с n степенями свободы становится ещё более громоздким. Для диссипативных систем с затуханием типа вязкого трения можно вве­сти матрицу рассеяния энергии 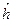и решать матричное уравнение

.

(8.27)

Собственные колебания, соответствующие , линейной диссипативной системы (8.27) можно искать в виде

.

(8.28)

Подставляя (8.28) в (8.27), получим уравнение степени 2 n для определения l

.

(8.29)

Так как уравнение (8.29) имеет действительные коэффициенты, то все его комплексные корни будут попарно сопряжёнными, т. е.

,   ,

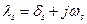где d_s и w_s - вещественные числа. Для диссипативной системы, не содержащей внутренних источников энергии, все d_s < 0. Общий вид свободных колебаний:

.

(8.30)

Для вынужденных колебаний по-прежнему разлагаем силу по векторам вида (8.23), а амплитуду вынужденных колебаний 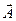- по векторам нормальных колебаний вида (8.22). Тогда

.

(8.31)

Таким образом, при совпадении частоты внешней силы с одной из собственных частот системы наблюдается резонанс. Однако амплитуда вынужденных колебаний при резонансе остается ограниченной, как и при резонансе в диссипативной системе с одной степенью свободы.