
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Собственные колебания в консервативных системах
|
|
Движение в системе с n степенями свободы описывается n независимыми координатами, выбор которых произволен. Число степеней свободы определяется минимальным числом переменных, необходимых для полного описания движения.
Можно также ввести нормальные координаты, число которых равно числу степеней свободы. Движение каждой нормальной координаты происходит независимо от остальных. Поэтому каждая нормальная координата совершает гармоническое колебание с собственной, или нормальной, частотой. Любые свободные и вынужденные колебания можно представить в виде суперпозиции нормальных колебаний.
Для исследования собственных колебаний в системе с n степенями свободы воспользуемся уравнениями Лагранжа. Пусть движение в системе определяется n независимыми обобщёнными координатами q 1, …, qn.
Потенциальная энергия системы является функцией обобщённых координат V (q 1, …, qn). В положении устойчивого равновесия потенциальная энергия имеет минимум, т. е.
 , s = 1, …, n,
, s = 1, …, n,
где qs 0 - значение координат в точке равновесия. Если в качестве новых координат выбрать xs = qs - qs 0 - отклонения от равновесных значений координат, то для малых xs можно записать

Потенциальная энергия определяется с точностью до постоянной, поэтому положим V (0, …, 0) = 0. Таким образом, пренебрегая высшими степенями в разложении, получим
 . .
| (8.1) |
Потенциальная энергия является положительно определённой квадратичной формой отклонения обобщённых координат от положения равновесия, ksl ³ 0, ksl = kls. Аналогично кинетическая энергия системы является положительно определённой квадратичной формой обобщённых скоростей:
 . .
| (8.2) |
В уравнениях (8.1) и (8.2) члены с s = l описывают энергию парциальных систем, а члены с s ¹ l соответствуют энергии связи между s -й и l -й парциальными системами.
Для каждой координаты можно записать уравнение Лагранжа (1.30) в виде
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 , s = 1, …, n,
, s = 1, …, n,
отсюда получим n линейных ДУ, которые могут быть записаны в матричной форме в виде
 . .
| (8.3) |
где матрицы массы  , упругости
, упругости  и вектор обобщённых координат
и вектор обобщённых координат  равны соответственно
равны соответственно
 ,
,  ,
,  .
.
Решение матричного уравнения (8.3) естественно искать в виде экспоненты
 ,
,
где амплитудный вектор 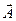 в общем случае может быть комплексным. Подставляя решение в уравнение, можно записать
в общем случае может быть комплексным. Подставляя решение в уравнение, можно записать
 . .
| (8.4) |
Нетривиальное решение матричного уравнения (8.4) возможно лишь при условии равенства нулю определителя системы
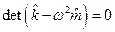 , ,
| (8.5) |
которое является уравнением n -й степени относительно w 2 и имеет n корней  , s = 1, …, n. Так как все коэффициенты уравнения (8.5) - действительные числа, тогда истинное решение на частоте ws следует искать в виде
, s = 1, …, n. Так как все коэффициенты уравнения (8.5) - действительные числа, тогда истинное решение на частоте ws следует искать в виде
 . .
| (8.6) |
Амплитудный вектор  должен удовлетворять уравнению вида (8.4):
должен удовлетворять уравнению вида (8.4):
 , s = 1, …, n. , s = 1, …, n.
| (8.7) |
Это матричное уравнение эквивалентно системе n однородных уравнений для амплитуд Asm. Первый индекс у амплитуды соответствует номеру собственной частоты, второй индекс - номеру координаты. Опять-таки, чтобы существовало нетривиальное решение, нужно, чтобы определитель последнего соотношения равнялся нулю. Если детерминант равняется нулю, то одну из амплитуд можно выразить через все остальные. Зафиксируем As 1, тогда сможем найти все остальные амплитуды, а соответственно и коэффициенты распределения амплитуд:
 , m = 1, …, n, s = 1, …, n.
, m = 1, …, n, s = 1, …, n.
Величины csm при фиксированном s образуют вектор  , который называется вектором коэффициентов распределения амплитуд на частоте ws, а все коэффициенты csm - квадратную матрицу:
, который называется вектором коэффициентов распределения амплитуд на частоте ws, а все коэффициенты csm - квадратную матрицу:
 .
.
Амплитудные вектора  и
и  выражаются через
выражаются через  следующим образом:
следующим образом:
 ,
,  .
.
Поэтому, подставляя эти соотношения в (8.6), получим s -е собственное колебание в виде
 . .
| (8.8) |
Каждая из функций вида (8.8) является решением (8.3). В силу принципа суперпозиции, общее решение нужно записать в виде взвешенной суммой (8.8):
 , ,  . .
| (8.9) |
В этом выражении Cs и js определяются начальными условиями, а формы собственных колебаний  и частоты ws зависят от параметров системы.
и частоты ws зависят от параметров системы.
Введём нормальные координаты, т. е. такие координаты, которые совершают гармонические колебания при любых начальных условиях. Их можно ввести следующим образом. Зададим n гармонических колебаний вида
 , s = 1, …, n.
, s = 1, …, n.
Каждое из колебаний hs можно рассматривать как нормальное колебание. Если так выделить нормальные колебания, то движение l -той координаты можно представить как
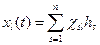 , l = 1, …, n. , l = 1, …, n.
| (8.10) |
Уравнения (8.10) выражают обобщённые координаты через нормальные. В матричном виде (8.10):
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 ,
,
где 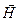 - вектор, образованный нормальными координатами.
- вектор, образованный нормальными координатами.
Подставим  в таком виде в (8.3), тогда
в таком виде в (8.3), тогда
 .
.
Так как каждая нормальная координата совершает гармоническое колебание, то для любого hs справедливо равенство
 ,
,
поэтому из двух последних соотношений следует:
 ,
,
т. е.  - диагональная матрица с элементами
- диагональная матрица с элементами  .
.
|
|
