Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Ортогональность нормальных колебаний и экстремальные свойства собственных частот

Каждому нормальному колебанию с частотой w_s соответствует опреде­ленное распределение амплитуд по координатам, или определённая форма колебаний. Формы колебаний, соответствующие разным собственным частотам, ортогональны друг другу. Для того, чтобы показать это, запишем уравнение (8.3) для s -й и r -й форм колебаний:

,   .

Умножим скалярно справа первое из этих уравнений на , а второе на . Учитывая, что матрицы и симметричны, т. е. , , вычтем из второго уравнения первое:

.

Если w_s ¹ w_r, то отсюда

.

(8.11)

С учётом формул (8.3) и (8.11) получаем также

.

(8.12)

Соотношения (8.11) и (8.12) называются условием ортогональности s -й и r -й форм нормальных колебаний. Использование условий ортогональности нормальных колебаний даёт возможность получить некоторые соотношения, общие для любых систем с n степенями свободы. Покажем, например, что потенциальная энергия любого собственного колебания равна сумме потенциальных энергий всех собственных колебаний. Потенциальную энергию системы (8.1) в матричной форме можно записать в виде

.

Подставляя теперь выражение вида (8.10) и учитывая условие ортогональности (8.12), получим

.

(8.13)

Аналогично с учётом условия ортогональности (8.11) легко показать, что

.

(8.14)

Выражения (8.13) и (8.14) показывают, что в нормальных координатах и потенциальная, и кинетическая энергия являются диагональными квадратичными формами. Следовательно, систему с п степенями свободы можно представить как набор из п независимых систем с одной степенью свободы.

Зададим в момент времени t = 0 произвольное отклонение от положения равновесия системы . Пусть скорости изменения координат в тот же момент времени равны нулю, т. е. . Тогда из уравнения (8.9) следует, что колебание в системе в любой момент времени t > 0 можно записать в виде

,   .

(8.15)

Потенциальная и кинетическая энергия системы при этом с учетом формул (8.11) и (8.12) равны

,   .

При колебаниях в консервативной системе среднее по времени значение потенциальной энергии равно среднему значению кинетической энергии, т. е.

.

(8.16)

Расположим собственные частоты в порядке их возрастания:

.

Если заменить все квадратом наинизшей частоты , то (8.16) превращается в неравенство

.

(8.17)

Левая часть неравенства (8.17) является функцией амплитуд C_s, т. е. функцией начального распределения амплитуд по степеням свободы. Величина является минимумом левой части (8.17) как функции . Таким образом, используя соотношение (8.15), получим

.

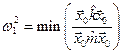(8.18)

Этот минимум достигается в том случае, когда все C_s, за исключением C ₁, равны нулю. Тогда , т. е. распределение амплитуд по координатам совпадает с первой собственной формой колебания. Для нахождения второй собственной частоты w ₂ следует выбрать начальное отклонение ортогональным первой собственной форме колебания, т. е.

и .

Тогда в выражении (8.16) суммирование начинается с s = 2 и самой низкой частотой окажется частота w ₂. Приводя рассуждения, аналогичные изложенным выше, получим

.

Минимум этого выражения достигается при , т. е. когда начальное распределение колебаний совпадает со второй собственной формой. Аналогичным образом можно найти все собственные частоты колебаний w _s и собственные формы (по индукции легко показывается, что все квадраты собственных частот являются экстремумами некоторых выраже­ний).