Крива розмагнічування та пряма повернення постійного магніту, їх апроксимація

Робоча діаграма постійного магніту, його енергія [Л.10, с. 156–162; Л., с. ]

Щоб отримати постійний магніт, необхідно намагнітити магнітно-твердий матеріал. Розглянемо кільцеве осердя з магнітно-твердого матеріалу [Л., с. ], на якому розташована обмотка з числом витків w, рис.4.

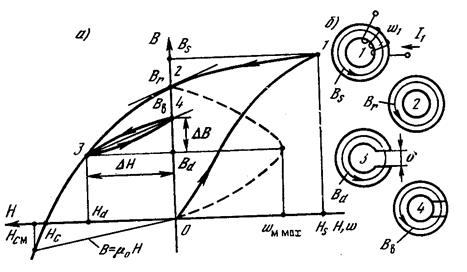
Рис. 4. Крива розмагнічування (а) і фізична модель (б) магніту

Якщо живити обмотку струмом І, достатнім, щоб довести осердя до насичення, то магнітний стан довільного елементу об’єму матеріалу буде характеризуватися робочою точкою 1 рис. 4. На кривій намагнічування, що має координати H_S, B_S. При цьому 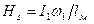, де 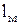– довжина середньої силової лінії в осерді.

Якщо від’єднати обмотку від мережі (І₁=0) (рис.4, б стан 2), то робоча точка переміститься по петлі гістерезису в точку 2 з координатами Н=0; В=В_V.

При цьому всередині осердя замикається магнітний потік Ф_V, який відповідає залишковій індукції В_V. Магнітні властивості магніту не виявляються зовні: питома магнітна енергія рівна 0 (рис.4, а).

Якщо розрізати осердя, ввівши проміжки (рис.4, б стан 3). Згідно з законом повного струму

H_dd + H_mm = 0.

Звідси напруженість в магніті

Н_m2 – Н × d / l_m < 0

Отже, при введенні повітряного проміжку відбувається розмагнічу­вання матеріалу. Робоча точка переміщується по кривій розмагнічування в точку 3. При певному проміжку ця точка може співпадати з точкою максимуму питомої енергії магніта в повітряному проміжку. Для більшого d більша від’ємна напруженість магніта і нижче по кривій розмагнічування знаходиться робоча точка.

Коли заповнити проміжок магнітно-м’яким матеріалом (рис.4, б, 4), то розмагнічу­вання матеріалу зменшиться. Проте внаслідок незворотності процесів перемагнічуван­ня, робоча точка переміститься вверх не по кривій намагнічування, а по лінії повернен­ня – по нижній частковій петлі гістерезису (рис.4, а). Коли вставки витягнути, робоча точка знову переміс­титься в положення 3, як по верхній частковій петлі гістерезиса. Так відбувається при прилеглих змінах зовнішнього розмагнічувального поля (напри­клад, при зміні Н = 0 ¸ Н_d). Але, як правило, часткову петлю за­мінюють прямою. Петля прямої повернення практично однакова, як і характеризується магнітною проникністю повернення m_в=DВ/DН. Набли­жено m_в знаходять за кутом нахилу дотичної до граничної петлі гістерезису в точці Н=0, В=В_V.

Апроксимація кривої розмагнічування і ліній повернення

Криві розмагнічування і лінії повернення лежать в основі розрахунку магнітних кіл з постійними магнітами. Однак згідно з нормативними документами, є тільки три нормовані точки кривої розмагнічування, без будь-яких даних про пряму повернення. Тому на практиці при дослідженні систем з постійними магнітами використовують розрахункові криві розмагнічування і лінії повернення, виражені в аналітичній формі.

1. Апроксимація рівнобічною гіперболою:

,

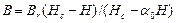де В і Н – біжучі координати (знак “–“ перед Н опускають); a₀ – залишковий коефіцієнт, що характеризує асимптоти гіперболи:

,

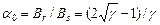де g – коефіцієнт форми кривої розмагнічування, що характеризує випуклість граничної петлі гістерезису:

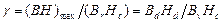
Рівняння лінії повернення може бути записане через координати точки відходу прямої повернення В₃, Н₃ (рис. 4, а):

,

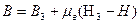або через залишкову індукцію повернення:

.

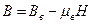Магнітну проникність магніта на прямій повернення приймати постійною

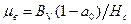
Приведена розрахункова крива розмагнічування

Для зручності розрахунків на практиці часто застосовується при дослідженні магнітоелектричних систем система відносних одиниць, де за базові приймають

– залишкову індукцію ;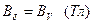

– коерцитивну силу 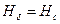А/м

площу нейтрального перерізу магніту перепендикулярну до силових ліній 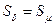(м²); довжина середніх силових ліній в магніті на один полюс 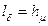(м).

Вторинними (похідними) базисними величинами є:

– МПС МП – ;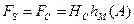

– магнітна проникність 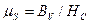(Гн/м);

– залишковий магнітний потік 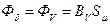(Цт);

– магнітний опір 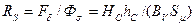(1/Гн);

– магнітна проникність 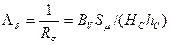(Гн);

– питома магнітна енергія 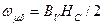(Дж/м²).

Магнітні величини в в.о. отримують діленням їх значень на відповідні базові: крива розмагнічування в в.о., називається приведеною кривою розмагнічування і для всіх магнітотвердих матеріалів проходить через точки Н_к=0, В_a=1 і Н_К=1, В_? =0, при цьому В^a=f(Н_a) співпадає з 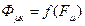. Рівняння розрахункової кривої з (1):

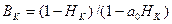
Для різних матеріалів ці криві відрізняються лише коефіцієнтами випуклості g (рис.5.).

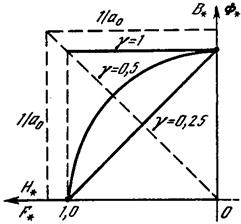
Рис. 5. Приведені розрахункові криві розмагнічування

При цьому відносна магнітна проникність

,

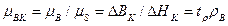де 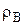– кут нахилу лінії повертання до осі абсцис.

Робоча діаграма магніту

ПМ в системах збудження ЕМ є не лише джерелом магнітного поля, але й частиною магнітопроводу. Однак енергія ПМ спостерігається в зовнішньому середовиші лише тоді, коли R_зовн.¹ 0. Зв’язок між парамет­рами ПМ і параметрами зовнішнього магнітного кола встановлюють за допомогою ДМ (як правило, для одного полюса). Розглянемо рис.7. –де є магніт у вільному стан і розвиває вільну МРС. – для підтримання магнітного потоку (точкою К) – перетин КР з МХ для проведення магнітного потоку (розсіяння) зовнішнього кола

,

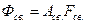де А_св. – МП магнітна провідність розсіяння магніта у вільному стані на один полюс.

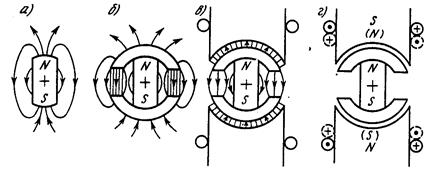
Рис.6.

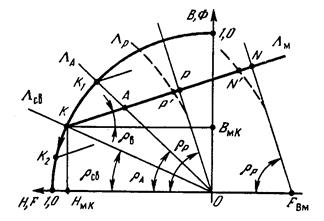
Рис.7.

В інженерній практиці використовується поняття МПР ПМ, приве­деної до МРС на робочій поверхні полюса магніту

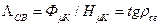
де Ф_mК – потік розсіювання у вільному стані, F_mK – МРС одного полюса; В_mK, Н_mK – координати точки К на ДМ. Введення приведеної провідності 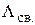дозволяє магнітну характеристику зовнішнього середовища представ­ляти у вигляді променя ОА_св. ОК кутом r_св.

Питома енергія ПМ в відносних одиницях для вільного стану дорівнює площі прямокутника Н_mККВ_mКО:

.

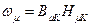Максимум електричної енергії матиме місце за умови

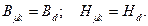
Отже, точка відходу ПП визначає ступінь використання енергії магніту.

Рис. 6.б. Якщо на полюси покласти окрмогупу з ПММ провідність з КМ збільшиться при цьому Р.Т на ДМ перміститься з К до А. Половина ПП визначається внутрішньою провідністю ПМ, що дорівнює у в.о. магнітній провідності повернення

L_м =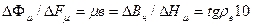

Точка L_А знаходиться на перетині ПП КL_м з променем ОL_А, проведеним під кутом r_А до ОХ

L_А =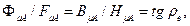

де L_А – провідність розсіяння ПМ з араматурою.

Зауважимо, що коли б магніт був намагніченим з арматурою, то хоча відходу ПП U₁ на перетині ОL_А з кривою розмагнічування.

Рис.6.в. Якщо магніт з арматурою розмістити між полюсами, то

L_р =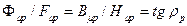

при цьому L_р > L_А > L_ав ; R_лр< R_A< R_mk.

За відсутності струму в обмотках, магнітний стан ПМ характеризується точкою Р.

Отже, МРС ПМ на відміну від електромагніта, не є постійною з зміною провідності ЗКМ. З ростом L МОС падає.

Якщо через обмотку пропустити паралельний струм, що створює МРС намагнічування, то потік в ПМ зросте до 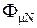згідно з прикладеною F_вм. Для визначення точки N досить перенести промінь ОL_р паралельно до самого себе вздовж осі ОХ на відрізок ОF_вм (див.рис.).

При певному струмі точка N займає положення, що відповідає насиченню магніта. При насиченні металевих пластин з МК, МХ стає нелінійною (пунктир на рис.).

Якщо, не доходячи до насичення, змінити напрям струму, то утвориться зовнішнє поле, що розмагнічує магніт, наприклад, до точки К₂, звідки переміщення вправо можливе лише по новій ПП.

Для підвищення стабільності властивостей постійних магнітів їх піддають стабілізації, тобто розмагніченню МРС дещо більшою, ніж максимально можлива робоча.

В ЕМ ПМ стабілізовані, тому РТ завжди знаходиться на ПП.

РДМ дає змогу встановити зв’язок між коефіцієнтом РТ і точки відходу ПП від кР.

Введемо поняття еквівалентності магнітної провідності ЗК ПМ

L_кс = Ф_к / F_к = В_к / Н_к = e_gr_kc.

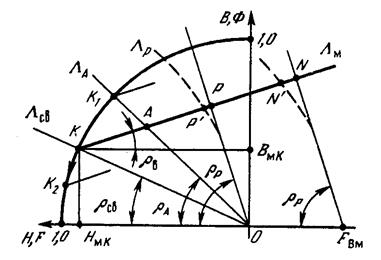
Рис.8.

Тоді, розв’язуючи рівняння МХ зовнішнього кола (В_р=L_рН_р) і рівняння ПП В = В_к + L_m(Н_к - Н) із врахуванням (S) маєм індукцію і напр. m п в точці р.

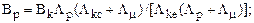
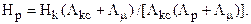
Питома енергія магніту в робочій точці

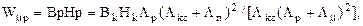
що справедливо при L_кс £ L_р. Максимум припадає на умову L_кс = L_р (тобто РТ на КР). Абсолютний максимум енергії при L_кс = L.О. або 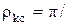4). Для приведеної кривої розмагнічування чисельно W_мmax = g.

У загальному випадку результуюча провідності Пм складається з Ld + L_s.

L_р = L_d + L_s

Отже, і енергію можна умовно розділити на енергію корисну і розсіяння

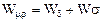, де питома корисна ЕН

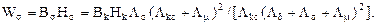
Максимум (при L_кс = const) енергії припадає на L_{d opt} = L_d + L_m..

Якщо L_кс = const (при фіксованій прямій ПМ)

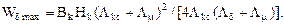
Якщо магніт стабілізований у вільному стані, то максимальна корисна енергія магніту

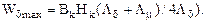
Аналітичні вирази кривої намагнічування постійних магнітів

Розрахунки магнітних кіл з постійними магнітами базуються на кривій розмагнічування, яку апроксимують аналітичним виразом. Для кривої розмагнічування постійних магнітів, виготовлених зі сплавів типу ЮНДК, аналітичним виразом є рівняння рівнобічної гіперболи у вигляді

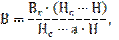
де B і H – біжучі координати.

Крива розмагнічування, побудована у відносних одиницях, називається зведеною кривою намагнічування. Для переходу від абсолютних значень параметрів магнітних матеріалів до відносних за базові одиниці приймають величини залишкової індукції 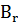та коерцитивної сили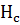

На основі рівняння зведеної кривої намагнічування матиме вигляд

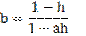
Постійні магніти з різними величинами 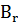і 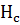, але однаковими коефіцієнтами форми γ (a залежить від γ), матимуть однакові зведені криві розмагнічування. Отже, зведена крива розмагнічування дає змогу оцінити у відносних одиницях форму кривої розмагнічування та ступінь її випуклості.

Для сплавів типу ЮНДК, коли невідомі проміжні точки кривої розмагнічування, можна будувати криву розмагнічування у відносних одиницях прийнявши наближено 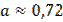(наведена на рис. 9). Координати точки на кривій розмагнічування, які відповідатимуть максимуму магнітної енергії, для сплавів типу ЮНДК визначатимуться співвідношеннями

Криві розмагнічування магнітнотвердих феритів та сплавів кобальту з рідкісноземельними металами є практично прямими, з якими збігаються прямі повернення. Для магнітів цих типів .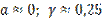

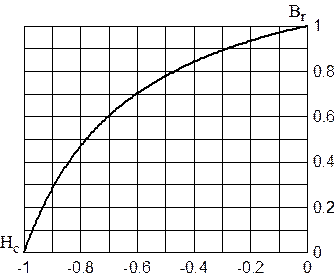
Рис. 9. Крива розмагнічування у відносних одиницях