💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Пересечение дислокаций

Пусть имеются две дислокации в различных плоскостях скольжения (рис.3.33): краевая АБ с осью вдоль Oz в плоскости скольжения x0z и неподвижная дислокация ВГ с осью вдоль Оу. После прохождения дислокации АБ через весь кристалл его верхняя часть смещается относительно нижней на b вдоль оси Ох, в том числе и часть ВВ' дислокации ВГ. Но так как линия дислокации не может прерываться внутри кристалла, то между нижней ГГ' и верхней ВВ' частями дислокации образуется двойной излом ВТ'. Этот излом будет перегибом, если вектор Бюргерса дислокации ВГ направлен вдоль Ох: b _ВГ= b_x, и ступенькой, если b _ВГ= b _z (рис. 3.33, б). Если дислокация АБ была винтовой с b = b_z, то, наоборот, при b _ВГ= b_x получается ступенька, а при b _ВГ= b_z – перегиб (рис.3.33, в).

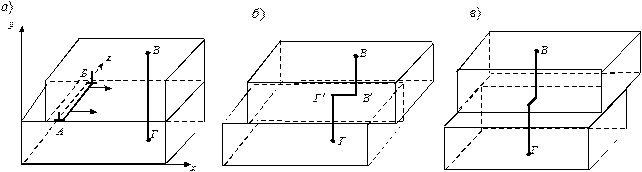
Рис. 3.33. Пересечение дислокаций: а – движение краевой дислокации АБ в плоскости xOz с вектором Бюргерса b = b _x навстречу неподвижной дислокации ВГ; б – результат прохождения дислокации АВ – сдвиг верхней полуплоскости на b и образование двойного излома В′ Г′ на дислокации ВГ; в – аналогичная картина после прохождения винтовой дислокации АБ

Радиус действия напряжений от ступеньки (или перегиба) высотой b порядка нескольких b: R = (2÷ 4) b. Подставив это значение в формулу для энергии дислокации, видим, что энергия каждой из дислокаций после пересечения увеличивается на величину

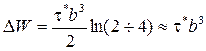. (3.49)

Следовательно, пересечение дислокаций требует дополнительных затрат энергии и приводит поэтому к упрочнению кристалла. Внешнее напряжение совершает работу при перемещении дислокации на Δ x = b, равную

А = τ b ² L, (3.50)

где L - длина этой дислокации.

Действительно, так как дислокации перпендикулярны, то их ядра, а следовательно, и область больших напряжений далеки друг от друга за исключением соприкасающихся при пересечении участков. Поэтому основной вклад в энергию взаимодействия, в отличие от взаимодействия параллельных дислокаций, вносят ядра дислокаций. Расстояние, на котором существенно взаимодействие дислокаций, порядка b: Δ x ≈ b.

Таким образом, условие энергетической выгодности пересечения дислокаций приобретает вид

А = τ b ² L > Δ W ≈ τ ^* b ³ или τ > τ 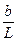^* , (3.51)

что очень похоже на условие работы источника Франка – Рида.

При

L < b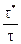

пересечение дислокаций энергетически невыгодно (они тормозятся друг на друге).

Таким образом, пересекающиеся дислокации взаимодействуют в основном только за счет ядер и на малых расстояниях, когда их ядра соприкасаются. Пересечение дислокаций приводит к увеличению их длины и, следовательно, требует дополнительных затрат энергии. Поэтому перемещение подвижных дислокации через неподвижные (дислокации «леса») требует добавочных напряжений, т. е. приводит к упрочнению тела.