Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Дислокационные реакции

Рассмотрим дислокационные реакции объединения двух или более дислокаций в одну и расщепление дислокации (разделение одной дислокации на две или более). Начнем с примера простейшей дислокационной реакции между двумя параллельными краевыми дислокациями (рис. 3.27).

Пусть обе дислокации двигались к точке В: первая с вектором Бюргерса b ₁ в плоскости АВ, вторая с вектором Бюргерса b ₂ в плоскости СВ. При их встрече в точке В происходит слияние их осей вдоль прямой, перпендикулярной плоскости АВС. Вектор Бюргерса дислокации, получившейся в результате такой дислокационной реакции, определяется из условия

b ₁ + b ₂ = b. (3.34)

Необходимо помнить, что невязка контура Бюргерса b является вектором, поэтому сложение векторов Бюргерса следует выполнять по правилу параллелограмма или треугольника (см. рис. 3.27, б). Рассмотрим энергетическую выгодность такой реакции в приближении линейного натяжения. Энергия дислокаций 1 и 2 в исходном состоянии (когда расстояние между ними велико и вкладом в энергию от их взаимодействия можно пренебречь) равна:

. (3.35)

В конечном состоянии

.

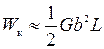Следовательно, слияние дислокации энергетически выгодно при условии

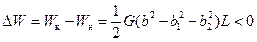или

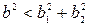, (3.36)

т. е. если угол между векторами b ₁ и b ₂ острый (α < π /2).

В приближении линейного натяжения условие дислокационной реакции всегда будет иметь вид (3.36). Для получения более точного результата надо учесть зависимость энергии от угла между l и b (если дислокации не краевые).

Если в реакцию вступают п параллельных дислокации 1, 2,..., п с вектором Бюргерса b ₁, b ₂,..., b _n, то аналогичный расчет для энергетической выгодности процесса даст

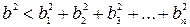. (3.37)

Частным случаем дислокационной реакции является аннигиляция двух дислокации противоположного знака, при которой b ₁=– b ₂ и b = b ₁+ b ₂=0. Для краевых дислокации аннигиляция означает объединение двух полуплоскостей в одну целую плоскость. При этом они исчезают и восстанавливается правильная решетка.

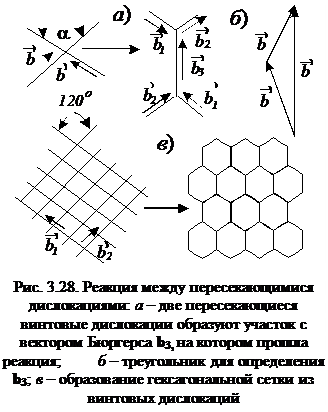
На рис. 3.28 показан случай другой реакции: две винтовые дислокации с 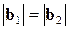, пересекающиеся под углом друг к другу. Если

,

то энергетически выгоден изгиб дислокационных линий около точки пересечения и образование участка, на котором происходит дислокационная реакция. Когда 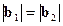, этот участок также будет винтовым (см. рис.3.28, б).

Если дислокации образуют сетки, состоящие из двух семейств винтовых дислокаций, и между ними будет идти реакция, то каждый узел сетки расщепится согласно схеме на рис. 3.28, а. При этом сетка из ромбической превратится в гексагональную. Если, между линиями дислокаций в исходном состоянии был угол 120°, то все гексагональные ячейки сетки будут правильными с равными сторонами и углами по 120°. Такие гексагональные сетки часто наблюдаются в кристаллах.

Кроме объединения нескольких дислокаций в одну, возможна и обратная реакция расщепления одной дислокации на две или более. Если геометрия решетки допускает расщепление дислокации с вектором Бюргерса b на две с векторами b ₁и b ₂, то рассуждения, аналогичные предыдущим, приведут к формуле энергетической выгодности данного процесса:

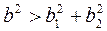или 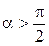. (3.38)

Обычно дислокации имеют наименьший из возможных векторов Бюргерса. Действительно, пусть имеется дислокация с вектором Бюргерса B= 2 b. Тогда для нее всегда выгодна реакция расщепления В → b + b, так как

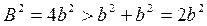. (3.39)

Энергетическое условие слияния или расщепления дислокаций является необходимым, но не достаточным условием, поэтому дело с рассматриваемым взаимодействием дислокаций обстоит сложнее. Используем для анализа энергетической выгодности слияния дислокаций условие Гельмгольца.

Пусть в исходном состоянии система имеет энергию

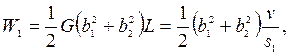
в конечном

,

а изменение энергии

,

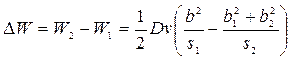где v - объем системы, s - площадь сечения дислокационной трубки, по которой интегрируют напряжения для определения энергии дислокации. Совершенно необязательно, что s = const.

Если слияние дислокаций выгодно при выполнении условия Гельмгольца 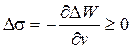, то при слиянии должно выполняться соотношение

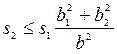. (3.40)

Промежуточные выводы:

1. Дислокация характеризуется двумя векторами – единичным вектором направления оси дислокации l и вектором Бюргерса b, направление которого характеризует направление смещений вблизи дислокации, а величина – мощность дислокации.

2. Дислокация является источником мощных и медленно спадающих упругих напряжений.

3. Пластическая деформация происходит в основном за счет перемещения дислокаций в теле.

4. Дислокация имеет высокую энергию порядка 1/2 Gb ³ на одну атомную плоскость.

5. Под действием внешних напряжений дислокации движутся так, что при этом площадь, по которой прошло скольжение, увеличивается.

6. Дислокации могут размножаться.

7. Дислокации могут вступать в реакции – объединяться или разделяться.