💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

От напряжения

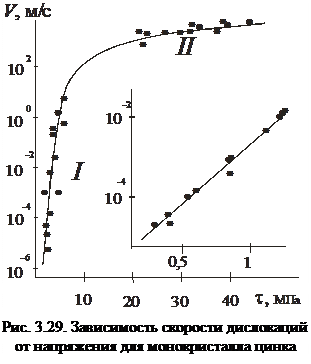
Результаты экспериментального исследования зависимости скорости дислокаций в плоскости скольжения от величины приложенного напряжения τ для монокристаллов цинка представлены на рис. 3.29. Аналогичные зависимости наблюдаются для других кристаллов. Эти закономерности позволяют сделать следующие заключения.

1. Напряжению τ соответствует скорость дислокации v, а не ее ускорение 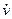, как это следовало бы из второго закона Ньютона 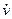= F/m (чем больше сила, тем больше ускорение, а не скорость). В повседневной жизни зависимость вида v=v (F) достаточно типична: постоянной силе, толкающей автомобиль, соответствует по­стоянная скорость автомобиля. Увеличение толкающей силы приводит к увеличению его скорости. Объяснение этого факта хорошо известно: существует сила сопротивления F _с движе­нию автомобиля, зависящая от его скорости v: F _с =F _c(v).Если автомобиль толкать с силой F, то скорость его увеличивается до тех пор, пока сила сопротивления не будет равна F: F = F (v). Отсюда находится постоянная скорость автомобиля при постоянной толкающей силе. При увеличении F до F ₁ скорость его растет до тех пор, пока новая сила сопротивления F _с(v) не будет равна F ₁. Время переходного режима – ускорения от v до v ₁ зависит от массы автомобиля. Очевидно, что движение дислокации определяется по тому же закону: должна существовать некая сила типа силы трения F _c(v), мешающая движению дислокаций в плоскости скольжения и возрастающая с увеличением их скорости.

Эту силу обычно называют силой внутреннего трения в отличие от внешнего трения (или просто трения), действующего на внешней поверхности металла. Сила внутреннего трения при перемещении дислокаций и других дефектов внутри объема тела ответственна за диссипацию (рассеяние) энергии деформации (переход упругой энергии в тепловую). Нагрев металла при обработке обусловлен одновременным действием обеих сил трения: поверхностные слои нагреваются в основном за счет внешнего трения, а внутренние – за счет внутреннего трения. Скорость дислокаций, как и в предыдущем примере, определяется равенством силы τ b, толкающей дислокацию в плоскости ее скольжения, и силы внутреннего трения F _c(v) на единицу длины дислокации:

F _c(v) = τ b. (3.41)

2. Оценим роль инерционных эффектов, зависящих от массы дислокации, т. е. определим переходное время, необхо­димое для увеличения скорости дислокации от v ₁ до v ₂ при увеличении напряжения от τ ₁ до τ ₂. Эффектив­ная масса дислокации (на единицу ее длины), определяющая ее инерционность, должна быть порядка Db ², где D – плот­ность кристалла.

Тогда характерное время, необходимое для разгона дислокации на D v=v ₂− v ₁:

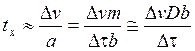, (3.42)

где а − ускорение.

Взяв данные для Δ v и Δ τ из рис. 3.29: при Δ τ =1 МПа D v =10² м/c, получим для b =3ּ 10 ^–10 м и D =10*10³ кг/м³ время t_х ≈ 3ּ 10^–10 с. Оно пренебрежимо мало для любых имею­щихся к настоящему времени экспериментов, во всяком слу­чае много меньше времени приложения нагрузки в любых реальных условиях. Таким образом, инерционные эффекты не играют никакой роли в динамике дислокации. Всегда можно считать, что скорость дислокации «равновесная», т. е. соот­ветствует равенству действующей силы и силы сопротивле­ния (3.41).

3. Видно, что кривая v (τ) состоит из двух различных уча­стков. На первом участке скорость дислокации быстро увеличивается с возрастанием напряжения, а на втором слабо зависит от τ. На первом участке зависимость v (τ) может быть аппроксимирована экспонентой типа v = v ₀exp(β τ), например,

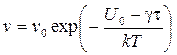, (3.43)

где v ₀ » 0, 1 С _зв, (С _зв - скорость звука в металле), U ₀ и γ – постоянные.

Таким образом, скорость на I участке экспоненциально возрастает с увеличением температуры: v ~ехр(– А/Т). Можно предположить, что на I участке дислокации движутся, преодолевая с помощью тепловых флуктуаций энергетические барьеры высотой U ₀ (например, барьер Пайерлса, барьеры из-за взаимодействия дислокаций с атомами примесей, барьеры при пересечении движущихся дислокаций и дислокаций других систем скольжения). Экспонента 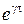описывает уменьшение высоты потен­циальных барьеров за счет действия касательных напряже­ний в плоскости скольжения.

4. Движение дислокации в I области может начаться до достижения напряжением τ в плоскости скольжения критического значения Пайерлса τ _П. Так, в приведенном примере наблюдается заметное движение дислокаций при τ ≈ 0, 2 МПа, в то время как τ _П> 10МПа.

5. Считается, что в области II дислокация теряет энергию в основном на возбуждение колебаний решет­ки, а препятствия, определявшие скорость дви­жения дислокации в области I, становятся несущественными. Поскольку вероятность такого возбуждения тем больше, чем интенсивнее собственные колебания решетки, то и сила сопротивления движению дислокации F _{с II} (v) возрастает с увеличением температуры. Такая сила называется дина­мическим трением. Точное значение F _{с II} (v) теоретически определить трудно.

В главе 1 мы показали, см. (1.6), что энергия межатомных связей в объеме металла описывается выражением, аналогичным соотношению Эйнштейна, связывающему скорость света и энергию системы. Отличие выражений состоит в том, что в качестве максимально достижимой скорости - скорости света для вакуума, в металле выступает скорость распространения звука С _зв. Возможно, что С _зв - это тоже максимально достижимая скорость, но не в вакууме, а в металле. Тогда и скорость дислокаций не может быть больше С _зв, что убедительно иллюстрирует рис. 3.29.