💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Рассмотрим п.4.

Данные, приведенные на рис. 3.29 свидетельствуют о том, что дислокация может двигаться при напряжениях, меньших, чем определяет потенциальный барьер Пайерлса. Считается, что потенциальный барьер для движения дислокаций может быть значительно снижен, если дислокация перемещается не по всей длине сразу, а выбрасывая вперед петли или, как их называют, перегибы.

В соответствии с принципом минимума энергии дислокация стремится ориентироваться вдоль направлений, по которым энергия ядра минимальна. Этому условию будут отвечать кристаллографические направления с минимальными индексами Мил­лера типа {110}, {110}, {111} и т. д. Различие в энергиях «правильно» и «неправильно» ориентированных дислокаций составляет приблизительно высоту барьера Пайерлса W­ _П, см. рис. 3.10.

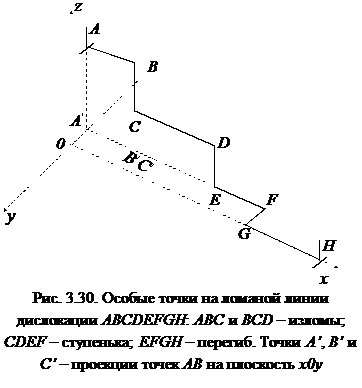На рис. 3.30 изображена ломаная дислокационная линия ABCDEFGH. Вектор Бюргерса дислокации b ≡ b_у, поэтому отрезки АВ, ВС, CD, DE, EF и GH являются краевыми, а отрезок FG — винтовым. Плоскостью скольжения дислокации является хОу, экстраплоскость совпадает с плоскостью хОz для отрезка GH и параллельна ей (отстоит на GF) для остальных краевых отрезков. Точки соединения длинных (больше b) отрезков АВ и ВС и ВС и CD - точки В и С называются изло­мами. Если два излома, например, D и Е или F и G, оказы­ваются на малом рас­стоянии друг от друга (DE, FG ≈ (1÷ 2) b), то они называются перегибами, если лежат в плоскости скольжения, или ступеньками, если они располагаются под углом к плоскости скольжения.

Так, на рис. 3.30 двойной излом DE является ступенькой, а FG – перегибом. На рис.3.31 изображено перемещение дислокационной линии из начального состояния АВ в конечное CD, отстоящее от начального на AC=BD ≈ b, за счет скольжения, а на рис. 3.32 - за счет переползания. Перемещение скольжением осуществляется серией по­следовательных перемещений перегиба EF вдоль оси дислока­ции. Элементарный акт такого смещения – перемещение EF в E'F' (EE=FF'≈ b) показан на рис. 3.31, б.

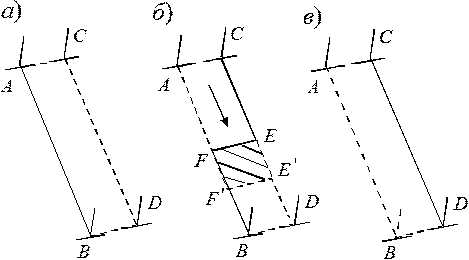
Рис. 3.31. Скольжение дислокаций как перемещение перегиба вдоль ее оси: а – исходное положение; б – промежуточная конфигурация; в – конечное положение. Перемещение перегиба из EF в E’F’ (EE’=FF’=b) – единичный (элементарный) акт скольжения дислокации

Движение пере­гиба вдоль дислокации, так же как и движение прямолиней­ной дислокации в плоскости скольжения, требует преодоле­ния некоторого энергетического барьера, называемого вторич­ным пайерлсовским W _П2 в отличие от обычного барьера Пайерлса W _П1. Расчеты и эксперимент показывают, что W _П2< < W _П1, т. е. перемещение перегиба происходит значительно легче, чем движение всей дислокации как единого целого одновременно.

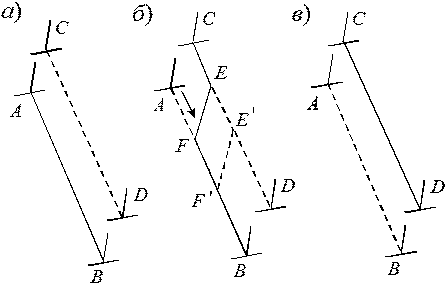
Рис. 3.32. Переползание дислокации как перемещение ступеньки вдоль ее оси

Движение дислокации при помощи двойного перегиба соответствует увеличению ее энергии

Δ W ≈ 2 W _пер0, (3.44)

где W _пер0 - энергия перегиба, учитывающая изменение энергии за счет увеличения протяженности дислокации при образовании «выброса» в новое положение, а также увеличение энергии «выбросов» за счет их «неправильной» ориентации, как лежащих в плоскостях с повышенной энергией. Для оценки энергии перегиба существует выражение 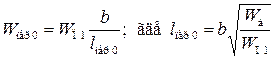- минимальная (равновесная) длина перегиба, соответствующая минимуму энергии дислокации с перегибом. Данные по значениям W _пер0 представлены в табл. 3.1.

Поскольку движение за счет парных перегибов сопровождается увеличением энергии дислокации, оно энергетически невыгодно. Считается, что источником дополнительной энергии для движения путем парных перегибов могут служить неравномерные поля внутренних напряжений, создаваемых другими дефектами, перемещающимися во время деформации, или тепловое движение атомов кристалла. Вероятность тепловой флуктуации в объеме равна

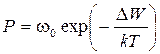, (3.45)

где D W − энергетический барьер; w₀ – характерная частота колебаний в рассматриваемом объеме; Т – температура, k − постоянная Больцмана. По­скольку в нашем случае ω ₀≈ 10¹³ с^–1 – частота колеба­ний атомов, то вероятность зарождения перегиба шириной l ≥ l ₀, который мог бы затем самостоятельно распространяться за счет ра­боты внешней силы, равна:

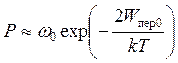.[В. В.4] (3.46)

Например, для алюминия 2 W _пер0 ≈ 0, 1 эв (см. табл. 3.1). При Т = 300° К вероятность Р _п равна:

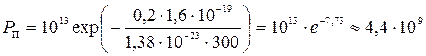с^–1. (3.47)

Если скорость дислокации рассчитать аналогично (2.27), то получим

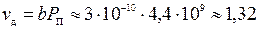м/с. (3.48)

При больших напряжениях τ > τ _П дислокации могут двигаться как целое и без помощи парных перегибов. Напротив, для кристаллов с высокими барьерами Пайерлса изменение скорости дислокаций при изменении температуры может быть очень большим в связи с температурной зависимостью скорости движения перегибов.