Расщепленные дислокации

До сих пор мы рассматривали дислокации, после прохождения которых через кристалл симметрия решетки полностью восстанавливается. Такие дислокации называются полными. Их вектор Бюргерса b ₀ должен удовлетворять условию трансляционной симметрии. Добавление этого вектора к координате любого атома п идеальной решетки r _n должно приводить к координате какого-либо другого атома п ₁ того же элемента:

r _n + b ₀= r _{n 1}. (3.52)

Практически, как это было показано ранее, существуют только дислокации с минимальными векторами Бюргерса, т. е. атомы n и п ₁ являются ближайшими соседями.

Кроме полных дислокаций существуют и частичные. Их вектор Бюргерса обычно меньше, чем у полной дислокации: b< b ₀. После прохождения частичной дислокации симметрия решетки восстанавливается не полностью, в плоскости скольжения за частичной дислокацией остается плоский дефект, чаще всего дефект упаковки. Рассмотрим подробнее вопрос о частичной дислокации на примере упорядоченного сплава, состоящего из 50% атомов А и 50% атомов В (рис. 3.34, а). Упорядочение такого сплава происходит из-за того, что энергия взаимодействия атомов А и В между собой W_AB меньше, чем энергии W_AA и W_BB, вследствие чего ближайшими соседями каждого атома являются атомы противоположного сорта.

Если в такой решетке пройдет дислокация, состоящая из одной полуплоскости, то она оставит за собой в плоскости скольжения дефект: атомы А окажутся напротив атомов А, а атомы В – напротив атомов В (рис. 3.34, б). Поскольку W_AB < (W_AA+W_BB)/2, то такая плоскость будет обладать избыточной энергией (в приближении взаимодействия ближайших соседей):

,

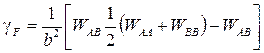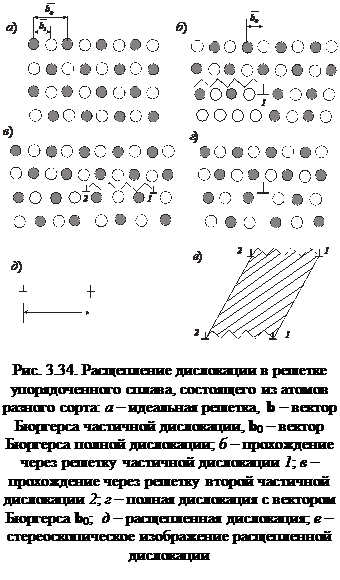т. е. образуется дефект, являющийся типичным дефектом упаковки, с удельной поверхностной энергией γ _F. Следовательно, такая дислокация с вектором Бюргерса b является частичной. Полная дислокация в такой решетке должна состоять из двух лишних полуплоскостей (рис. 3.34, г) и иметь вектор Бюргерса b ₀=2 b.

Этот результат можно было бы получить сразу, зная атомное строение идеальной решетки. Действительно, вектор b, добавленный к координате любого атома, переводит его в неэквивалентное положение: атом А в положение атома В и наоборот. Только вектор b ₀ = 2 b удовлетворяет условию трансляционной симметрии, т. е. переводит все атомы в эквивалентные положения.

На рис. 3.34, б видно, что движение второй частичной дислокации 2 в той же плоскости скольжения уничтожает в ней дефект упаковки, создаваемый первой частичной дислокацией 1. Следовательно, две частичные дислокации 1 и 2 с дефектом упаковки между ними эквивалентны одной полной дислокации (см. рис. 3.34, г). Такой дефект, когда две частичные дислокации с дефектом упаковки между ними эквивалентны полной дислокации, называется расщепленной дислокацией. В более сложных случаях расщепленная дислокация может состоять из трех, четырех и т. д. частичных дислокаций и сооветственно из двух, трех и т. д. полосок дефектов упаковки.

Рассмотрим расщепление дислокации – превращение полной дислокации в расщепленную (рис. 3.34, г, д, в). Энергия полной дислокации

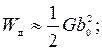(3.53)

энергия расщепленной дислокации

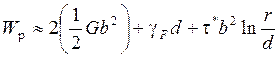, (3.54)

где d – расстояние между частичными дислокациями. Первый член в этом выражении описывает энергию частичных дислокаций, более точно он равен 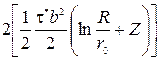, см. раздел 3.6, второй – энергию дефекта упаковки, третий – энергию взаимодействия (отталкивания) частичных дислокаций. Чем больше расщепление дислокации, тем больше энергия дефекта упаковки, но тем меньше энергия их взаимодействия (при d=b≈ r ₀ второй член несуществен и W _p =W_b). Таким образом, дефект упаковки стягивает, а упругое взаимодействие отталкивает частичные дислокации. Следовательно, должно существовать некоторое равновесное расщепление, соответствующее равенству сил притяжения и отталкивания. Найдем это равновесное расщепление d ₀ из условия минимума энергии :

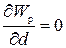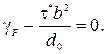(3.55)

Отсюда

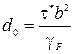, (3.56)

или, учитывая эмпирическое соотношение

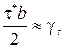, (3.57)

где γ _s – удельная поверхностная энергия,

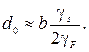(3.58)

Таким образом, при малых энергиях дефекта упаковки γ _F < < γ _s расщепление дислокации будет большим в атомном масштабе d ₀> > b.