Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Функция графигінің дөңестігі, ойыстығы және иілу нүктелері

Анық тама. Егер 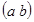интервалында дифференциалданатын 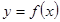қ исығ ының барлық нү ктелері сол қ исық қ а жү ргізілген жанамадан жоғ ары орналасса, онда онда қ исық ты осы аралық та ойыс (дө ң естігі тө мен қ арағ ан) дейді, ал 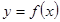қ исығ ының барлық нү ктелері сол қ исық қ а жү ргізілген жанамадан тө мен орналасса, онда қ исық ты осы аралық та дө ң ес (дө ң естігі жоғ ары қ арағ ан) дейді. Қ исық тың ойыс жә не дө ң ес бө лігін бө ліп тұ ратын нү ктені иілу нү ктесі деп атайды.

Теорема. 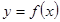функциясы 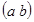интервалында екі рет дифференциалданатын болсын. Егер осы интервалдың ә рбір нү ктесінде 1) болса, онда функцияның графигі бұ л интервалда дө ң ес болады; 2) 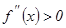болса, онда функцияның графигі бұ л интервалда ойыс болады

4-мысал. 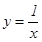гиперболасы (0, +¥) интервалында ойыс болады, себебі 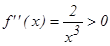, ал (–¥, 0) интервалында дө ң ес, себебі .

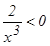Теорема (иілу нү ктесінің қ ажетті шарты). Егер 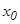нү ктесі 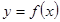функциясының иілу нү ктесі болса, онда бұ л нү ктеде функцияның екінші туындысы нө лге тең, яғ ни 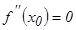. Функцияның екінші туындысы нө лге айналатын немесе екінші туындысы болмайтын нү ктелер екінші текті кү дікті нү ктелер деп аталады. Функцияның иілу нү ктесін осы кү дікті нү ктелердің арасынан іздеу керек.

Теорема (иілу нү ктенің жеткілікті шарты). Егер 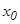нү ктесінен ө ткенде функцияның екінші туындысы таң басын ө згертсе, онда 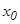нү ктесі иілу нү ктесі болады.