Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сеть массового обслуживания

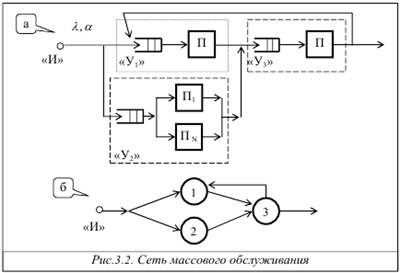
Сеть массового обслуживания (СеМО) – совокупность взаимосвязанных СМО, в среде которых циркулируют заявки (рис.3.2, а).

Основными элементами СеМО являются узлы (У) и источники заявок (И).

Узел сети представляет собой систему массового обслуживания.

Источник – генератор заявок, поступающих в сеть и требующих определенных этапов обслуживания в узлах сети.

Для упрощенного изображения СеМО используется граф СеМО.

Граф СеМО – ориентированный граф, вершины которого соответствуют узлам СеМО, а дуги отображают переходы заявок между узлами (рис.3.2, б). Переходы заявок между узлами СеМО, в общем случае, могут быть заданы в виде вероятностей передач.

Путь движения заявок в СеМО называется маршрутом.

2. Параметры СеМО

Для описания линейных разомкнутых и замкнутых однородных экспоненциальных СеМО используется следующая совокупность параметров:

• число узлов в сети: n;

• число обслуживающих приборов в узлах сети: K₁,..., K_n;

• матрица вероятностей передач: P = [ p_ij | i, j = 0, 1, …, n], где p_ij – вероятность передачи заявки из узла i в узел j;

• интенсивность λ ₀ источника заявок, поступающих в разомкнутую СеМО (РСеМО), или число заявок M, циркулирующих в замкнутой СеМО (ЗСеМО);

• средние длительности обслуживания заявок в узлах сети: b₁, …, b_n.

Заметим, что состав параметров разомкнутых и замкнутых СеМО различается только одним параметром, а именно: для ЗСеМО, в отличие от РСеМО, вместо интенсивности λ ₀ поступления заявок в сеть необходимо задать число постоянно циркулирующих в сети заявок M.

Для линейных СеМО элементы матрицы вероятностей передач должны удовлетворять условию:

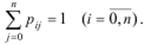(3.24)

Это условие отражает тот факт, что любая заявка, покинувшая некоторый узел, обязательно (с вероятностью 1) перейдёт в какой-то узел, включая тот же самый или нулевой. Переход заявки в нулевой узел означает, что заявка покинула сеть.

В случае неэкспоненциальных разомкнутых СеМО дополнительно необходимо задать законы распределения или, по крайней мере, вторые моменты интервалов времени между поступающими в разомкнутую сеть заявками и длительностей обслуживания заявок в узлах сети.

В случае неоднородных СеМО необходимо дополнительно задать количество классов заявок H в сети и для каждого класса – матрицы вероятностей передач P(h), интенсивности λ ₀(h) или число заявок M(h), а также средние длительности обслуживания b_i(h) заявок класса h =1, H в узле i =1, n. При необходимости могут быть заданы законы распределений интервалов между поступающими в РСеМО заявками и законы распределений длительностей обслуживания заявок разных классов в узлах сети.

ВЫВОД

Любая заявка, покинувшая некоторый узел, обязательно (с вероятностью 1) перейдёт в какой-то узел, включая тот же самый или нулевой. Переход заявки в нулевой узел означает, что заявка покинула сеть.