💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Характеристики и свойства ДО БП

При бесприоритетной ДО средние времена ожидания одинаковы для всех классов заявок и определяются по следующей формуле:

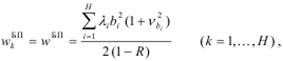(4.9)

где 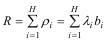– суммарная загрузка системы.

Выражение (4.5) получено в предположении, что в системе существует стационарный режим и отсутствует перегрузка: R < 1.

Анализ представленной аналитической зависимости (4.5) позволяет выявить свойства ДО БП и сформулировать следующие выводы.

1. Среднее время ожидания заявок разных классов при использовании ДО БП одинаково при любых интенсивностях поступления λ ₁, …, λ _H и законах распределений B₁(τ), …, B_H(τ) длительностей обслуживания заявок: w_k^БП = w^БП для всех k =1, …, H. Отметим, что средние времена пребывания в системе заявок разных классов, в общем случае, различны, так как различны длительности обслуживания: u_k^БП=w^БП + b_k k= (1, …, H).

2. Среднее время ожидания заявок в очереди минимально при постоянной (детерминированной) длительности обслуживания заявок каждого класса, когда коэффициент вариации длительности обслуживания =0, и увеличивается с ростом коэффициента вариации (дисперсии) длительности обслуживания. Заметим, что зависимость среднего времени ожидания от коэффициента вариации носит нелинейный характер.

Так, например, при экспоненциально распределенной длительности обслуживания, когда 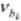= 1, среднее время ожидания заявок увеличивается в 2 раза, а при 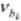= 2 – в 5 раз, по сравнению с детерминированным обслуживанием.

3. Среднее время ожидания заявок существенно зависит от суммарной нагрузки Y (загрузки R) системы (рис.4.6, а). При Y ≥ 1 (R → 1) время ожидания заявок всех классов возрастает неограниченно: w^ПБ→ ∞, то есть заявки могут ожидать обслуживания сколь угодно долго. Отметим, что увеличение суммарной нагрузки может быть обусловлено двумя факторами: увеличением интенсивностей поступления в систему заявок разных классов или увеличением длительности обслуживания заявок (например, за счет уменьшения скорости работы обслуживающего прибора).

Зависимость среднего времени пребывания в системе заявок разных классов от суммарной нагрузки аналогична зависимости времени ожидания (рис.4.6, б). Единственное отличие состоит в том, что средние времена пребывания в системе заявок разных классов, в общем случае, различны, то есть u_i ≠ u_j (i ≠ j), поэтому на графике, в отличие от времени ожидания, могут отображаться несколько зависимостей. Это различие обусловлено различием длительностей обслуживания заявок разных классов.

Аналогично, на графиках, отображающих зависимости средних длин очередей и числа заявок в системе от суммарной нагрузки, в общем случае, будут изображаться несколько кривых, соответствующих разным классам заявок. Отметим, что средние длины очередей заявок разных классов, несмотря на одинаковое время ожидания, в общем случае, различны и, в соответствии с формулой Литтла (l_i = λ _iw^БП), совпадают только в случае равенства интенсивностей поступления заявок разных классов в систему.

4. Можно показать, что для бесприоритетной дисциплины обслуживания в обратном порядке (ООП), когда заявки на обслуживание выбираются по правилу «последний пришёл – первый обслужен», средние времена ожидания заявок будут такими же, как и при обслуживании в порядке поступления (ОПП), но дисперсия времени ожидания будет больше. Это обусловлено тем, что заявки, поступившие последними, будут ожидать незначительное время, в то время как заявки, попавшие в начало очереди, могут ожидать обслуживания достаточно долго, что обусловливает большой разброс значений времени ожидания.

5. Аналитическое исследование дисциплины обслуживания в циклическом порядке (ДО ЦП) достаточно сложно и связано с громоздкими математическими выкладками. Поэтому, не выписывая громоздких формул, отметим лишь наиболее характерные особенности, присущие этой ДО.

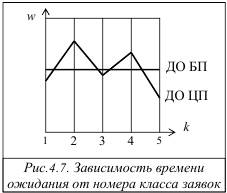Для дисциплины обслуживания в циклическом порядке среднее время ожидания заявок разных классов в общем случае не одинаково (рис.4.7).

Это различие зависит от соотношения параметров потоков (λ ₁, …, λ _H) и обслуживания (B₁(τ), …, B_H (τ)) заявок разных классов. В некоторых случаях ДО ЦП позволяет обеспечить меньшую суммарную длину очереди заявок, чем ДО БП. Зависимость среднего времени ожидания заявок каждого класса от суммарной нагрузки Y имеет такой же вид, как и для ДО БП (рис.4.6).

2. Характеристики и свойства ДО ОП

Приоритеты называются относительными, если они учитываются только в момент выбора заявки на обслуживание и не сказываются на работе системы в период обслуживания заявки любого класса (приоритета). Относительность приоритета связана со следующим. После завершения обслуживания какой-либо заявки из очереди на обслуживание выбирается заявка класса с наиболее высоким приоритетом, поступившая ранее других заявок этого класса (такого же приоритета). Если в процессе её обслуживания в систему поступят заявки с более высоким приоритетом, то обслуживание рассматриваемой заявки не будет прекращено, то есть эта заявка, захватив прибор, оказывается как бы более приоритетной. Таким образом, приоритет относителен в том смысле, что он имеет место лишь в момент выбора заявок на обслуживание и отсутствует, если прибор занят обслуживанием какой-либо заявки.

Введение относительных приоритетов (ОП) позволяет уменьшить по сравнению с ДО БП время ожидания высокоприоритетных заявок.

При описании свойств для определённости будем полагать, что относительные приоритеты назначены по правилу: «более высокий приоритет – классу заявок с меньшим номером».

Для ДО ОП среднее время ожидания заявок класса k определяется по следующей формуле:

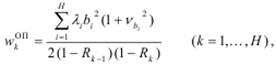(4.10)

где R_{k− 1} и R_k – суммарные загрузки, создаваемые заявками, которые имеют приоритет не ниже (k − 1) и k соответственно:

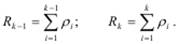(4.11)

Анализ представленной зависимости (4.10) позволяет выявить свойства ДО ОП и сформулировать следующие выводы.

1. Введение относительных приоритетов по сравнению с ДО БП приводит к уменьшению времени ожидания высокоприоритетных заявок первого класса и к увеличению времени ожидания низкоприоритетных заявок класса H: w₁^ОП < w₁^БП и w_H^ОП > w_H^БП.

2. При использовании ДО ОП средние времена ожидания заявок монотонно увеличиваются с уменьшением приоритета при любых интенсивностях поступления λ ₁, …, λ _H и законах распределения B₁(τ), …, B_H (τ) длительностей обслуживания: w₁^ОП < w₂^ОП < …< w_H^ОП.

Отметим, что для средних времён пребывания заявок разных классов последнее соотношение, в общем случае, может и не выполняться.

Свойства, сформулированные выше, иллюстрируются рис.4.8, а, показывающим характер зависимости среднего времени ожидания заявок w_k от номера класса k при использовании ДО БП и ДО ОП.

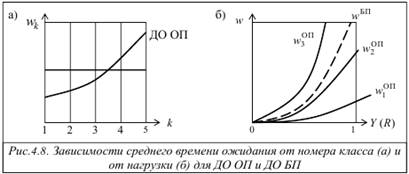3. На рис.4.8, б показаны зависимости среднего времени ожидания заявок разных классов от суммарной нагрузки Y системы при использовании ДО ОП. Здесь же для сравнения приведена аналогичная зависимость для ДО БП (штриховая линия). Характер зависимостей свидетельствует о том, что для ДО ОП при Y → 1 резко увеличивается время ожидания заявок низкоприоритетных классов, в то время как для высокоприоритетных заявок это увеличение незначительно. Более того, для высокоприоритетных заявок обеспечивается достаточно хорошее качество обслуживания, то есть небольшое время ожидания даже при возникновении перегрузок, когда суммарная нагрузка становится больше единицы: Y ≥ 1. Это свойство, называемое защитой от перегрузок, обеспечивается за счет отказа в обслуживании низкоприоритетным заявкам, время ожидания которых при этом резко возрастает. При ДО БП защита от перегрузок отсутствует для всех классов заявок.

4. Рассмотрим более детально свойство защиты от перегрузок при ДО ОП, для чего построим зависимости среднего времени ожидания заявок трех классов при значительном росте нагрузки Y (рис.4.9).

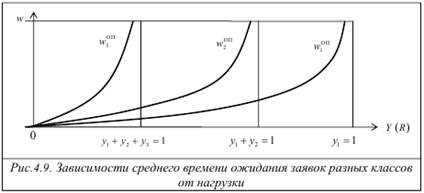
При достижении суммарной нагрузки, создаваемой заявками всех трех классов, значения 1 (y1 + y2 + y3 = 1) время ожидания заявок 3-го класса устремляется в бесконечность, что означает отказ в обслуживании, при этом заявки классов 1 и 2 продолжают обслуживаться и имеют конечное время ожидания. Дальнейшее увеличение нагрузки приводит к отказу в обслуживании заявок второго класса при y1 + y2 =1, то есть когда создаваемая заявками 1-го и 2-го классов нагрузка достигнет значения 1. Заявки первого класса получат отказ в обслуживании при y1 =1. Таким образом, в отличие от ДО БП при ДО ОП система полностью перестаёт обслуживать заявки, то есть функционировать, только в том случае, если нагрузка, создаваемая заявками самого высокоприоритетного (первого) класса, достигнет значения 1.

ВЫВОД

Для бесприоритетной дисциплины обслуживания в обратном порядке (ООП), когда заявки на обслуживание выбираются по правилу «последний пришёл – первый обслужен», средние времена ожидания заявок будут такими же, как и при обслуживании в порядке поступления (ОПП), но дисперсия времени ожидания будет больше.