Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Электроны в кристаллической решетке.

Электроны в кристаллической решетке будем рассматривать как идеальный одноатомный газ. Решение уравнения Шредингера для значения энергии электрона можно получить из уравнения Шредингера.

Рассмотрим одномерный случай:

.

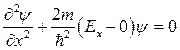Полагая, что электроны не взаимодействуют между собой:

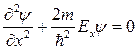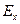, - состояние энергии вдоль оси .

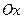Это уравнение по своей форме совпадает с уравнением свободных колебаний. Решение этого уравнения: , где .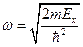

Рассмотрим граничные условия:

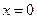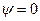: будет удовлетворять этому требованию.

.

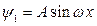С другой стороны при 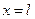, 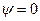будет в случае, если .

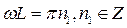Тогда

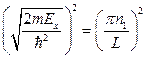
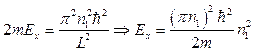
Аналогично мы получаем:

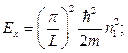
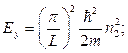
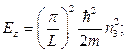
Полная энергия: 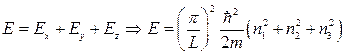, где 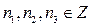- параметры или квантовые числа (энергия электрона определяется четырьмя квантовыми числами).

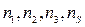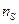( - спин, квантовое число).

Если рассматривать электронный газ, то спектр разрешенных значений энергии состоит из множества близко расположенных дискретных уровней.

В действительности валентные электроны в кристалле двигаются не вполне свободно. На них действует периодично поле кристаллической решетки. Это приводит к тому, что спектр возможных значений энергии валентных электронов распадается на ряд чередующихся разрешенных и неразрешенных зон. Вместо одного одинакового для всех 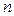электронов уровня возникает 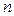очень близких, но не совпадающих уровней.

Т.о. каждый уровень изолированного атома распадается в кристалле на 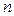густо расположенных уровней, образующих полосу или зону.

на каждом уровне может находиться два электрона за счет .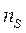

Существование энергетических зон позволяет объяснить с единой точки зрения существование металлов, полупроводников и диэлектриков.

Разрешенная зон возникает из того уровня, на котором находятся валентные электроны в основном состоянии. Атомы называются валентной зоной. В зависимости от степени заполнения валентной зоны электронами и ширины запрещенной зоны, возможны три случая:

1)

Свободная зона: подуровни не заняты.

Валентная зона: подуровни не все заняты.

В этом случае достаточно сообщить электронам небольшую энергию порядка 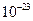эВ для того, чтобы перевести их на более высокие уровни.

Дополнительная энергия, вызванная действием на электрон внешнего Эл. поля, оказывается достаточной для перевода электрона на более высокий уровень. Т.е. электроны могут ускоряться эл. полями. Кристаллы с такой структурой называются проводниками.

2)

В валентной зоне электроны занимают все уровни, и свободных уровней нет.

Энергия такого движения 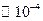эВ.

3)

Валентная зона вся занята.

В случаях 2) и 3) уровни в зонах полностью заняты электронами. Если ширина 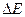невелика, десятые доли эВ, то энергия теплового движения достаточна для перевода частиц электронов в свободную зону. Такие кристаллы относятся к типу полупроводников. Если 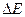(случай 3)) велика, порядка нескольких эВ, то тепловое движение не может перевести электроны в свободную зону. Такие вещества называются диэлектриками. (диэлектрики могут проводить только при высоких температурах).