Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Излучение и поглощение абсолютно черного тела.

Абсолютно черным телом называется такое тело, которое полностью поглощает падающее на него излучение. Это весьма абстрактное понятие. Примером абсолютно черного тела может быть сферическая полость, зеркально отражающейся поверхности.

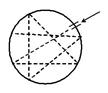Наша сфера поглотила, но не отразила луч.

Возьмем уголек и раскалим его. Поместим его внутрь нашей сферы. Уголек излучает электромагнитные волны.

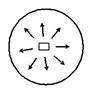Они будут отражаться от зеркала внутри поверхности и частично поглощаться угольком. Наступает равновесное состояние, при котором энергия, которую излучает уголек за единицу времени.

= той энергии, которую уголек поглощает. В таком состоянии система может находиться довольно долго.

Сделаем дырочку. Через это отверстие. Излучение, характеризуемое для равновесного состояния, будет выходить с помощью специальных приборов.

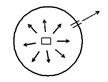В частности можно определить распределение энергии по частотам излучения.

Эту задачу решили в начале прошлого века (в частности нем. экспериментатор Вин получил кривую).

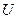– энергия, приходящаяся на конкретную частицу единицу объема.

Попытки получить выражение для 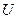в рамках классической модели теоретически оказалось безуспешным. В частности Релей и Джинс получили формулу

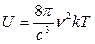- Релея – Джинса.

Т.е. согласно теории функция 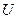должна меняется по параболе с ростом частоты. Это действительно имеет место, но для небольших значений частот.

Релей и Джинс перепроверяли свою формулу неоднократно. Однако оказалось, что они все делали верно. Сложившаяся ситуация называлась ультрафиолетовая катастрофа.

В 1900г. немецкий физик М. Планк сумел подобрать формулу, которая хорошо описывает эти кривые. В отличие от Релея и Джинса формула выглядела так:

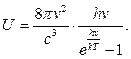
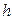- некоторая константа, значение которой можно было определить из кривых Вина = 6, 62*10^-34 Дж.

Анализируя эту формулу можем выделить некоторую порцию энергии 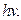Планк выдвинул идею о том, что энергия при излучении поглощается и излучается порциями 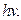По Планку атом излучает порцию энергии, которая потом распространяется в виде волны, а затем снова поглощается атомами.

Эйнштейн далее развивал идеи Планка и утверждает, что энергия не только поглощается и излучается порциями, но и распространяется в виде квантов.

Т. о. в полости, внутри которой находится раскаленный уголек в равновесном состоянии со своим излучением, в рамках квантовой модели находится фотонный газ (состоящий из частичек фотона) в равновесном состоянии при конкретной температуре.

По своей природе фотоны являются бозонами, поэтому на них распространяется статистика Бозе.

В рамках этой модели получили выражение для формулы Планка.

Выделим некоторую частоту 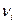и интеграл частот .

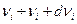Выражение для фазового объема:

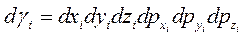
Проинтегрируем данное выражение по пространственным координатам.

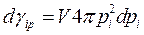
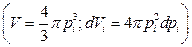
Физический смысл: сферический слой толщиной 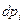, радиусом .

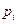Учитывая принцип неопределенности Гейзенберга 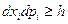, выделим наименьший фазовый объем , соответствующий одному 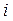- тому квантовому состоянию.

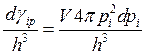- число квантовых состояний, соответствующих частоте .

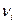Если домножить это выражение на 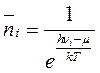(химический потенциал бозонов равен нулю):

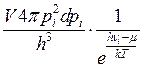- число частиц фотонов в шаровом слое.

Домножим на энергию одного фотона :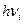

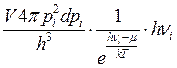- энергия в шаровом слое, соответствует частоте .

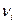Если разделим все это на 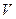, то получим выражение для энергии, приходящейся на частоту 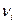в единице объема:

.

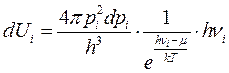Когда определяли число частиц, надо было учесть, что фотонов в два раза больше, из-за двух возможных способов поляризации.

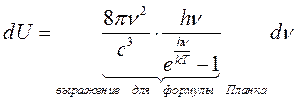
Если проинтегрировать это выражение по частотам от 0 до 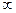, то мы получим энергию, приходящуюся на все частоты.

.

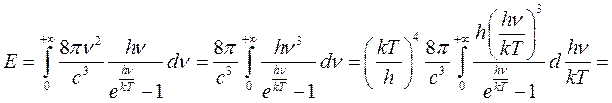
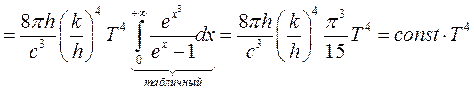Полная энергия, приходящаяся на все частоты при излучении абсолютно черного тела 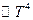. Это находится в полном согласии с экспериментальным законом Стефана – Больцмана, согласно которому энергия, излучаемая с единицы поверхности в единицу времени пропорциональна .

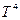Теоретически этот экспериментальный закон невозможно вывести в рамках классической физики, и выведен нами в рамках модели квантовой физики.

Закон смещения Вина (будет рассмотрен на практике).

В заключении покажем, что из формулы Планка вытекает формула Рэлея – Джинса.

Возьмем формулу Планка

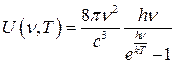
и вспомним: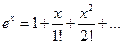

Если взять область небольших значений частот, то 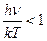, то в разложении ряда можно ограничиться первыми двумя слагаемыми:

.

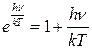Подставляя это выражение в формулу Планка:

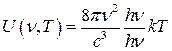- совпадает с формулой Рэлея – Джинса.

Итак, в области малых частот формула Рэлея – Джинса правильна.