
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение ОДУ и их систем операционным методом.
|
|
РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Постановка задачи
При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему. Лучше всего это делать в виде дифференциальных уравнений (ДУ) или системы дифференциальных уравнений. Наиболее часто они такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) – теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.
Обыкновенным дифференциальным уравнением (ОДУ) n-го порядка называется следующее уравнение, которое содержит одну или несколько производных от искомой функции y(x):
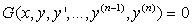 , здесь y(n) обозначает производную порядка n некоторой функции y(x), x – это независимая переменная.
, здесь y(n) обозначает производную порядка n некоторой функции y(x), x – это независимая переменная.
В ряде случаев дифференциальное уравнение можно преобразовать к виду, в котором старшая производная выражена в явном виде. Такая форма записи называется уравнением, разрешенным относительно старшей производной (при этом в правой части уравнения старшая производная отсутствует):
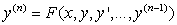 (6.1)
(6.1)
Именно такая форма записи принята в качестве стандартной при рассмотрении численных методов решения ОДУ.
Линейным дифференциальным уравнением называется уравнение, линейное относительно функции y(x) и всех ее производных.
Например, ниже приведены линейные ОДУ первого и второго порядков
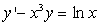
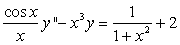
Решением обыкновенного дифференциального уравнения называется такая функция y(x), которая при любых х удовлетворяет этому уравнению в определенном конечном или бесконечном интервале. Процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.
Общее решение ОДУ n-го порядка содержит n произвольных констант C1, C2, …, Cn
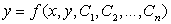
Это очевидно следует из того, что неопределенный интеграл равен первообразной подынтегрального выражения плюс константа интегрирования
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
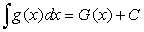
Так как для решения ДУ n-го порядка необходимо провести n интегрирований, то в общем решении появляется n констант интегрирования.
Частное решение ОДУ получается из общего, если константам интегрирования придать некоторые значения, определив некоторые дополнительные условия, количество которых позволяет вычислить все неопределенные константы интегрирования.
Точное (аналитическое) решение (общее или частное) дифференциального уравнения подразумевает получение искомого решения (функции y(x)) в виде выражения от элементарных функций. Это возможно далеко не всегда даже для уравнений первого порядка.
Численное решение ДУ (частное) заключается в вычислении функции y(x) и ее производных в некоторых заданных точках 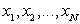 , лежащих на определенном отрезке. То есть, фактически, решение ДУ n-го порядка вида получается в виде следующей таблицы чисел (столбец значений старшей производной вычисляется подстановкой значений в уравнение):
, лежащих на определенном отрезке. То есть, фактически, решение ДУ n-го порядка вида получается в виде следующей таблицы чисел (столбец значений старшей производной вычисляется подстановкой значений в уравнение):
| X | y | y' | y(n-1) | |
| x1 | y(x1) | y'(x1) | … | y(n-1)(x1) |
| x2 | y(x2) | y'(x2) | … | y(n-1)(x2) |
| xN | y(xN) | y'(xN) | … | y(n-1)(xN) |
Например, для дифференциального уравнения первого порядка таблица решения будет представлять собой два столбца – x и y.
Множество значений абсцисс 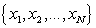 в которых определяется значение функции, называют сеткой, на которой определена функция y(x). Сами координаты при этом называют узлами сетки. Чаще всего, для удобства, используются равномерные сетки, в которых разница между соседними узлами постоянна и называется шагом сетки или шагом интегрирования дифференциального уравнения
в которых определяется значение функции, называют сеткой, на которой определена функция y(x). Сами координаты при этом называют узлами сетки. Чаще всего, для удобства, используются равномерные сетки, в которых разница между соседними узлами постоянна и называется шагом сетки или шагом интегрирования дифференциального уравнения
 или
или 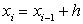 , i = 1, …, N
, i = 1, …, N
|
|
