
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные свойства преобразования Лапласа.
|
|
Преобразова́ ние Лапла́ са — интегральное преобразование, связывающее функцию \ F(s) комплексного переменного (изображение) с функцией \ f(x) вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Свойство линейности. Для любых постоянных чисел α и β
L{α x(t)+β y(t)}=α L{x(t)}+β L{y(t)}
Преобразование суммы равно сумме преобразований. Постоянный множитель можно вынести за знак преобразования.
2) Дифференцирование оригинала при нулевых начальных условиях. Если X(p)=L{x(t)} и начальные условия нулевые, т.е.
x(0)= x(1)(0) = x(2)(0) =…= x(n–1)(0)=0, то:
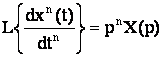
Дифференцирование оригинала при нулевых начальных условиях соответствует умножению изображения на p.
3) Интегрирование оригинала.
Если X(p)=L{x(t)} и x(t)=0 при t< 0, то
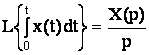
Интегрирование оригинала соответствует делению изображения на переменную p.
4) Теорема запаздывания. Если X(p)=L{x(t)}, то для любого положительного числа τ
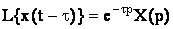
Функция x(t– τ) представляет собой функцию x(t) сдвинутую во времени вправо на величину τ или другими словами запаздывающую на величину τ (время запаздывания).
5) Теорема о начальном значении оригинала.
Значение оригинала x(t) в момент начала отсчета врмемни t=0 определяется по его изображению X(p) по формуле:
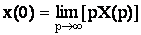
6) Теорема о конечном значении оригинала.
Предел к которому стремится оригинал x(t) при t→ ∞ определяется по его изображению X(p) по формуле:
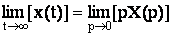
|
|
