Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Числовые ряды с положительными членами. Признак Даламбера.

Признак сходимости Даламбера

Жан Лерон Даламбер – это знаменитый французский математик 18-го века. Вообще, Даламбер специализировался на дифференциальных уравнениях и на основании своих исследований занимался баллистикой, чтобы у Его Величества лучше летали пушечные ядра. Заодно и про числовые ряды не забыл, не зря потом шеренги наполеоновских войск так четко сходились и расходились.

Перед тем как сформулировать сам признак, рассмотрим важный вопрос:
Когда нужно применять признак сходимости Даламбера?

Сначала начнем с повторения. Вспомним случаи, когда нужно применять самый ходовойпредельный признак сравнения

Основные же предпосылки для применения признака Даламбера следующие:

1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 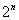, , 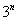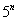и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.

2) В общий член ряда входит факториал. С факториалами мы скрестили шпаги ещё на уроке Числовая последовательность и её предел. Впрочем, не помешает снова раскинуть скатерть-самобранку:





…


…

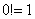
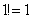
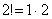
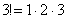
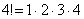
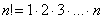
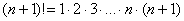
! При использовании признака Даламбера нам как раз придется расписывать факториал подробно. Как и в предыдущем пункте, факториал может располагаться вверху или внизу дроби.

3) Если в общем члене ряда есть «цепочка множителей», например, 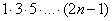. Этот случай встречается редко, но! При исследовании такого ряда часто допускают ошибку – см. Пример 6.

Вместе со степенями или (и) факториалами в начинке ряда часто встречаются многочлены, это не меняет дела – нужно использовать признак Даламбера.

Кроме того, в общем члене ряда может встретиться одновременно и степень и факториал; может встретиться два факториала, две степени, важно чтобы там находилось хоть что-тоиз рассмотренных пунктов – и это как раз предпосылка для использования признака Даламбера.

Признак Даламбера: Рассмотрим положительный числовой ряд 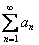. Если существует предел отношения последующего члена к предыдущему: 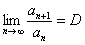, то:
а) При 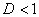ряд сходится. В частности, ряд сходится при .
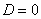б) При 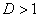ряд расходится. В частности, ряд расходится при .
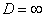в) При 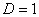признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.

У кого до сих пор проблемы с пределами или недопонимание пределов, обратитесь к уроку Пределы. Примеры решений. Без понимания предела и умения раскрывать неопределенность 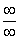дальше, к сожалению, не продвинуться.

Достаточные признаки сходимости числовых рядов с положительными членами.

Признак Даламбера.

Теорема. Рассмотрим ряд 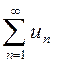с положительными членами и предел отношения последующего члена ряда к предыдущему.

1) Если 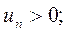2) существует 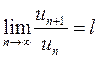, тогда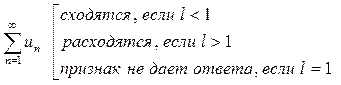

Доказательство:

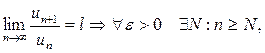
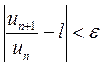то есть .

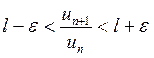Рассмотрим 3 случая:

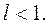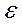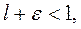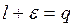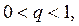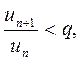
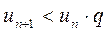1) Выберем столь малым, чтобы значение тогда, полагая , при значении имеем для .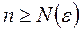

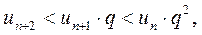
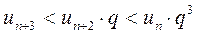и так далее.

Члены ряда 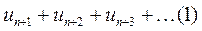меньше членов геометрической прогрессии: 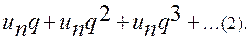Так как 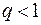, то ряд (2) сходится, значит, по теореме сравнения сходится и ряд (1).

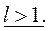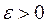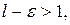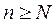
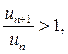
2) Возьмем столь малым, что тогда при 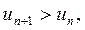члены ряда не 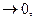не выполняется необходимый признак сходимости 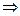ряд расходится.

3) 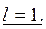Покажем, что в этом случае ряд может как сходиться, так и расходиться.

1) гармонический ряд 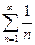расходится, для него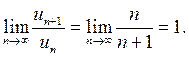

2) Рассмотрим ряд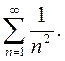

Для него 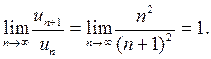Сравним члены исследуемого ряда со сходящимся рядом 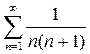(доказано ранее).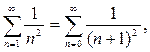

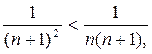
Значит, 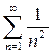сходится.