Вейвлет-анализ. Применение к обработке изображений

Обработка изображений, в частности, полученных от цифровых фотокамер и сканеров, обычно выполняется с помощью специализированных программных средств (PhotoShop, CorelDRAW и др.). В них профессионально реализованы многие математические методы обработки изображений. Их можно применять, ничего не зная о сути этих методов, так же, как пользоваться телевизором, не разбираясь в радиотехнике.

Пример работы в среде графического пакета CorelDRAW 10 приводится на рис. 14.22.

Рис. 14.22. Пример файла вейвлет-формата WI в графическом редакторе CorelDRAW 10

Из приведенного рисунка видно, что в сжатом вейвлет -формате файл занимает на диске около 220 Кбайт, а в памяти развернут до 2, 2 Мбайт. Как правило, качество графических файлов в этом формате заметно выше, чем в других графических форматах. Однако часто возникают задачи, при решении которых необходимо знать суть применяемого метода вейвлет -преобразования и уметь пользоваться этим преобразованием. При этом можно использовать системы компьютерной математики (Mathcad, Maple, MATLAB).

Из теории сигналов известно, что произвольный сигнал s (t) можно представить в виде взвешенной суммы простых составляющих – базисных функций ψ _k (t), помноженных на коэффициенты C_k:

. (14.122)

Так как базисные функции ψ _k (t) предполагаются заданными как функции вполне определенного вида, то только коэффициенты C_k содержат информацию о конкретном сигнале. Таким образом, можно говорить о возможности представления произвольных сигналов на основе рядов общего вида (14.122) с различными базисными функциями. Например, хорошо известные синусоидальные функции легли в основу рядов Фурье. Синусоиды-гармоники периодических сигналов предельно локализованы в частотной области, вырождаясь на спектрограммах в вертикальные линии, но не локализованы вообще во временной области – они определены в интервале времен от -¥ до +¥. Подобное определение является теоретической абстракцией. Поэтому ряды Фурье плохо пригодны для представления коротких локальных особенностей сигналов и функций, содержащих скачки и перепады. Более того, ряды Фурье в классическом виде принципиально непригодны для представления нестационарных сигналов. В связи с этим ученые искали иные базисы для разложения сигналов.

В начале 90-х годов было обнаружено, что такие достаточно универсальные базисы существуют, и им дали названия вейвлетов. Термин вейвлет (wavelet) в переводе с английского означает «короткая или маленькая волна» или «волночка». На основе совокупности таких волн, перемещаемых и масштабируемых, и зародилась техника вейвлет-преобразований.

Простейший вейвлет Хаара (однократная волна прямоугольной формы) имеет вид

Он был известен еще в 1910 г., но тогда никто не догадывался, что он является новым базисом декомпозиции произвольных функций и сигналов с возможностью их абсолютно точного восстановления. Затем были открыты десятки новых и старых вейвлет-функций, причем реализация большинства из них возможна только итерационными и программными методами.

Рассмотрим пример применения вейвлетов Хаара. Пусть имеется сигнал, представленный целочисленными компонентами вектора (9 7 3 5). Это могут быть, например, значения пикселей некоторой строки изображения. Разрешение в этом случае равно 4. Перейдем к более грубому (вдвое меньшему) разрешению 2, для чего вычислим среднее из каждой пары компонентов сигнала. Получим вектор (8 4) с двумя детализирующими коэффициентами (1 -1). Они представляют половину от приращений уровня относительно среднего значения, т. е. (9-7)/2 = 1 и (3-5)/2= - 1. Прибавив и отняв первый коэффициент от первого компонента вектора огрубленного сигнала – числа 8, получим компоненты 9 и 7. Аналогично, прибавив и отняв -1 от второго компонента вектора огрубленного сигнала 4, получим 3 и 5, т. е. вторую пару компонентов исходного вектора. Продолжим огрублять сигнал вдвое и перейдем к разрешению 1. Наш вектор превратится в (6) с детализирующим коэффициентом 2. Его прибавление и вычитание дадут вектор (8 4). Окончательно, для декомпозиции (разложения) исходного сигнала имеем:

Следовательно, для представления сигнала достаточно хранить его грубое значение 6 и детализирующие коэффициенты 2, 1 -1. Операции с ними задаются видом вейвлета Хаара. Так, на уровне разрешения 1 он представляется двумя функциями – аппроксимирующей с уровнем 1 и детализирующей с уровнем +1 на первой половине периода и -1 на второй половине периода (именно это задает сначала сложение, а затем вычитание детализирующего коэффициента). В результате, осуществления композиции сигнала и использование последнего (самого грубого) аппроксимирующего коэффициента и ряда детализирующих коэффициентов точно восстанавливается значение сигнала. Процедуры изменения разрешения вдвое в ходе композиции и декомпозиции реализуют так называемый диадический метод. Он является разновидностью более общего кратномасштабного метода и лежит в основе устранения избыточности, свойственной непрерывным вейвлет-преобразованиям.

Смысл такого представления состоит в том, что осуществлен переход от представления независимых значений сигнала к его приращениям. Коэффициенты вейвлет-представления реальных сигналов часто существенно меньшие числа, чем представления отсчетов сигналов. Для реальных сигналов многие коэффициенты по уровню оказываются настолько малыми, что их можно отбросить. Это дает возможность значительно сократить объем информации о сигнале, выполнить его компрессию и очистку от шумов. В настоящее время имеется множество более интересных вейвлетов, что обеспечивает обширный выбор базисных функций как для точного, так и приближенного представления любых сигналов. Точное представление сигнала реализуют только ортогональные вейвлеты. Условие ортогональности двух вейвлетов ψ _i (t) и ψ _k (t) имеет вид:

, (14.123)

где δ _ik – символ Кронекера.

В литературе имеется детальное описание свойств вейвлетов, в том числе и ортогональных. В частности, кроме вейвлета Хаара, к ним относятся вейвлеты Добеши, для прямого и обратного преобразований которых имеются встроенные функции в среде Mathcad.

Как и в случае преобразований Фурье, возможны два вида вейвлет-преобразований – прямое и обратное. Прямое означает вейвлет-декомпозицию сигнала, т. е. его разложение по базису вейвлетов. В основе непрерывного вейвлет-преобразования лежит использование двух непрерывных и интегрируемых по всей оси t (или x) функций:

- вейвлет-функция psi ψ (t) с нулевым значением интеграла

,

определяющая детали сигнала и порождающая детализирующие коэффициенты;

- масштабирующая или скейлинг-функция phi φ (t) с единичным значением интеграла:

,

определяющая грубое приближение (аппроксимацию) сигнала и порождающая коэффициенты аппроксимации.

Phi-функции φ (t) присущи только тем вейвлетам, которые относятся к ортогональным. Psi-функция ψ (t) создается на основе той или иной базисной функции ψ ₀(t), которая, как и ψ (t), определяет тип вейвлета. Базисная функция должна удовлетворять всем требованиям, которые предъявляются к psi-функции ψ (t). Она должна обеспечивать выполнение двух операций:

смещения по оси времени t – ψ ₀(t-b) при b Î R;

масштабирования a ^-1/2ψ ₀(t / a) при a > 0 и a Î R ⁺ - {0}.

Параметр a задает ширину этого пакета, а b – его положение, R – задает область определения параметров, в общем случае бесконечную (верхний индекс + означает положительную, а обозначение – {0} исключение нулевой точки).

В литературе часто вместо времени t используется аргумент x, а вместо параметров a и b используются иные обозначения.

Нетрудно убедиться в том, что следующее выражение задает сразу два требуемых свойства функции ψ (t):

. (14.124)

При заданных a и b функция ψ (t) и есть вейвлет. Вейвлеты являются вещественными функциями времени t и колеблются вокруг оси t (или х). Парметр b задает положение вейвлетов, а параметр a - их масштаб. О вейвлетах, четко локализованных в пространстве (или во времени), говорят, что они имеют компактный носитель.

Прямое непрерывное вейвлет-преобразование сигнала s (t) задается, по формальной аналогии с преобразованием Фурье, путем вычисления вейвлет-коэффициентов по формуле:

. (14.125)

Если сигнал ограничен во времени a, b Î R, a ≠ 0, то интегрировать можно в конечных пределах:

. (14.126)

Обратное вейвлет-преобразование задается выражением:

(14.127)

и обеспечивает восстановление сигнала.

На практике непрерывное изменение параметров a и b вызывает избыточность вейвлет-представления сигналов. Поэтому, как и в примере с вейвлетом Хаара, используется кратномасштабный (в частности диадический) метод.

В современных версиях системы Mathcad (2000/2001 и более поздние) включены простые функции дискретных волновых преобразований:

- wave(V) – дискретное волновое преобразование действительных чисел с использованием четырех коэффициентного волнового базиса Добеши. Вектор V должен содержать 2 n действительных значений, где n – целое число;

- iwave(V) – обратное преобразование относительно преобразования wave(V – вектор с числом элементов 2 n).

Эти функции реализуют пирамидальный алгоритм быстрого вейвлет-преобразования.

На рис. 14.31 приводится пример вейвлет-преобразования сигнала или временного ряда с безразмерным шагом по времени, условно равным 1. В этом примере над произвольным сложным сигналом (трапецеидальный импульс, на который наложены компоненты синусоидального и прямоугольного сигналов с меняющейся во времени частотой, и шум, заданный генератором случайных чисел), представленным 512 точками, осуществляется прямое, а затем обратное вейвлет-преобразование, в результате чего исходная весьма сложная временная зависимость практически полностью восстанавливается. Об этом свидетельствует величина погрешности, вычисленная в программе рис. 14.31.

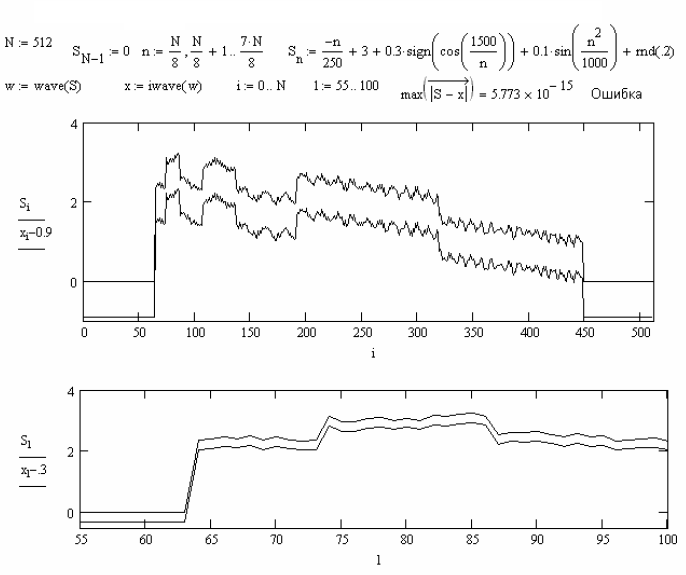
Рис. 14.31. Пример дискретного вейвлет-преобразования

В нижней части рисунка построены (в двух масштабах) графики исходного синала и сигнала, прошедшего прямое и обратное вейвлет-преобразование. (Сигналы настолько близки, что на рисунке их пришлось раздвинуть по вертикали.)

Вейвлет-преобразование с его иерархическим базисом хорошо приспособлено для анализа каскадных процессов, турбулентных сигналов, фрактальных и мультифрактальных множеств, имеющих иерархическую природу.

Примеры использования вейвлет-преобразований:

- тонкая обработка изображений и их запись в файлы (уже реализована в различных графических пакетах, например, CorelDRAW 10/11);

- компрессия сигналов с целью передачи сигналов по линиям с малой пропускной способностью, например, модемным линиям Интернета;

- выявление новых закономерностей в сигналах и изображениях;

Области применения вейвлетов внастоящее время интенсивно расширяются. Для осуществления вейвлет-преобразований в реальном масштабе времени уже созданы специальные микросхемы.