Описание межатомного взаимодействия в материалах. Первопринципные методы.

Каким бы ни был конкретный метод атомистического моделирования, для изучения процессов, происходящих в материалах на атомарном уровне, необходимо прямо или опосредованно знать законы взаимодействия между отдельными атомами. В зависимости от того, каким образом задаются эти законы, атомистические методы можно разделить на два основных класса.

В методах первого класса потенциальная энергия атомов и взаимодействие между ними описываются аналитическими функциями атомных координат. При этом, численные коэффициенты функций определяются путем подгонки предсказаний различных физических величин, получаемых с использованием данного потенциала, к экспериментально определенным значениям для изучаемых систем (например, упругие модули, фононные спектры, температура плавления, поверхностная энергия и т.п.). Такие методы и сами потенциалы взаимодействия часто называют эмпирическими или полуэмпирическими. Очевидно, чем больше свойств материала описывает эмпирический потенциал, тем шире область его применимости. В последнее время, наряду с экспериментальными данными, для создания потенциалов межатомного взаимодействия используют данные квантово-механических расчетов, особенно в случаях, когда потенциалы предназначаются для описания таких объектов, для которых экспериментальные данные просто отсутствуют. В современной научной литературе можно найти многочисленные рекомендации и методические схемы по созданию новых потенциалов межатомного взаимодействия для конкретных материалов.

Эмпирические потенциалы широко используются в материаловедческих исследованиях, особенно в рамках таких вычислительных методов, как молекулярная динамика и, в меньшей степени, кинетическом Монте-Карло. Ранее они активно использовались и для оценки энергий образования и барьеров миграции различных точечных дефектов. Однако точность таких предсказаний была невелика, а полученные результаты, как правило, сильно отличались от предсказаний более точных квантово-механических методов, описываемых ниже. Поэтому в настоящее время, более принята обратная процедура, когда данные квантово-механических расчетов точечных дефектов используются для оптимизации создаваемых эмпирических потенциалов.

Эмпирические потенциалы разрабатываются для конкретных материалов или классов материалов. К настоящему времени разработано много различных потенциалов, особенно для чистых (одноэлементных) материалов. Для многокомпонентных материалов эмпирические потенциалы разрабатываются, как правило, только для имеющих важное практическое применение композиций, поскольку создание даже одного потенциала требует значительных расчетных усилий по выбору и обоснованию конкретного вида потенциала, подгонке коэффициентов и проверке качества потенциала для предсказания свойств материала, напрямую не использовавшихся в процессе определения коэффициентов. Принято группировать эмпирические потенциалы по принадлежности к нескольким классам, в зависимости от физической модели, лежащей в их основе. В настоящее время металлические системы предпочтительно моделировать с использованием потенциалов относящихся к классу «метод внедренного атома» (англ. embedded atom method или EAM), ковалентные системы методами типа Абеля-Терсоффа, напрямую учитывающими направленность ковалентных связей, а изоляторы и ионные кристаллы – методами, принимающими во внимание зарядовые состояния и кулоновское взаимодействие составляющих материал ионов.

Возможность задания законов взаимодействия между атомами в аналитическом (либо табулированном) виде позволяет изучать динамическое поведение расчетных ячеек, содержащих миллионы атомов. Это обуславливает широкое применение эмпирических потенциалов и вычислительных методов на их основе. Однако не следует забывать, что достоверность предсказаний этих методов очень существенно зависит от того, данные о каких свойствах материала были использованы при подборе параметров потенциала. Попытки использования потенциалов за пределами области, для которой они создавались, могут приводить к неадекватным предсказаниям. Например, эмпирические потенциалы, хорошо воспроизводящих равновесные свойства кристаллических решеток, могут быть совершенно непригодны для исследования аморфных модификаций того же самого материала, а потенциалы для твердых тел часто плохо описывают расплавы. И конечно, эмпирические потенциалы не могут помочь нам получить информацию об электронных свойствах изучаемого материала, что является критическим моментом при исследовании, например, полупроводниковых материалов или материалов, обладающих выраженными магнитными свойствами.

Для того, чтобы уйти от необходимости эмпирического описания взаимодействия между атомами, весьма привлекательно использование методов второго класса, называемых обычно первопринципными (или ab initio) методами. Методы этого класса исходят из того, что взаимодействие между атомами обеспечивается электронами, а поведение электронов однозначно описывается законами квантовой механики. Поэтому для описания межатомного взаимодействия достаточно знать решения основных квантово-механических уравнений (уравнения Шредингера или в более сложном варианте – уравнения Дирака) для электронов в поле ядер атомов. Дополнительным бонусом такого решения является возможность автоматически получить детальное представление об электронной структуре изучаемых твердых тел.

К сожалению, прямолинейная реализация этой задачи, даже с учетом мощности современных компьютеров, оказывается возможной в лучшем случае для небольших молекул, состоящих из достаточно легких атомов. Действительно, атомы содержат десятки, а то и сотни электронов, так что для описания даже сотни атомов приходится рассматривать тысячи и десятки тысяч электронов. Уравнения квантовой механики для многоэлектронных систем крайне сложны для решения в силу их нелинейности и принципиальной необходимости учитывать взаимодействия всех атомов и электронов между собой. Тем не менее, введение упрощающих предположений позволяет свести описание поведения электронов к таким моделям, которые еще достаточно точно описывают поведение электронов и взаимодействие атомов, но уже по силам вычислительным машинам. Как правило, чем больше вводится упрощений и допущений, тем большие системы становится возможным описывать, но и тем больше потеря точности. Наиболее точные квантово-механические методы могут быть применены для расчетов небольших атомных ансамблей (до 1000 атомов), тогда как довольно грубые приближения позволяют моделировать системы, состоящих из нескольких тысяч атомов.

На рис. 14.2 представлена диаграмма, которая показывает соотношение уровней сложности моделирования и допустимого числа атомов в моделируемой системе для различных первопринципных методов. Максимальное число атомов в расчетной ячейке, доступное для того или иного метода, представляет собой грубую оценку того, насколько большой атомный ансамбль может быть рассчитан за разумное время (как правило - несколько дней) на современных компьютерах. Хотя, строго говоря, время расчета зависит не только от числа атомов в расчетной ячейке, но и от других параметров, влияющих не точность расчета. Для сравнения на той же диаграмме показаны возможности эмпирических методов, которые позволяют моделировать системы, содержащие до десятков миллионов атомов. Разумеется, размеры изучаемых систем постепенно увеличиваются по мере роста доступных компьютерных мощностей и эффективности самих компьютеров. То, что десять лет назад воспринималось как передовой край вычислительного эксперимента, сегодня является рутинным исследованием.

Рис. 14.2. Соотношение между уровнем сложности моделирования и максимальным числом атомов в системе для различных вычислительных методов, где HF - метод Хартри-Фока, DFT – теория функционала плотности, TB -метод сильной связи.

Условно можно разделить квантово-механические методы на следующие группы:

• Квантовое Монте-Карло (англ. Quantum Monte Carlo или QMC). Наиболее точный, но и наиболее требовательный к вычислительным ресурсам метод. С увеличением числа атомов N в расчетной ячейке вычислительные затраты растут почти экспоненциально, причем скорость роста зависит не только от N, но и от других параметров, например - от температуры системы. В результате методы квантового МК могут быть использованы только для расчетов небольших молекул и фактически относятся к разряду квантово-химических методов, а в материаловедческих задачах почти не применяются.

• Метод Хартри-Фока (англ. Hartree-Fock или HF). В рамках этого метода используется упрощенное описание системы электронов, в котором отброшена часть эффектов электронного взаимодействия, но достаточно аккуратно учитывается наиболее важное электростатическое взаимодействие и явным образом принимается во внимание действие принципа Паули, который запрещает нахождение в одной и той же точке двух электронов с идентичным набором квантовых чисел. Вычислительные затраты растут ~ N ⁴ или быстрее, в зависимости от того, как учитывается корреляция между электронами. Как видно на рис. 14.2, пределы применимости данного метода ограничиваются, в настоящее время, десятками атомов, что также практически исключает непосредственное применение данного метода к решению материаловедческих задач.

• Метод теории функционала плотности (англ. Density Functional Theory или DFТ). Метод является наиболее распространенным на сегодняшний день первопринципным методом, используемым в материаловедческих задачах. Метод использует более грубые приближения для описания взаимодействия между электронами, чем метод Хартри-Фока, но зато не отбрасывает полностью ни один из аспектов этого взаимодействия. Характерной особенностью метода является выражение всех функциональных зависимостей для энергии электронов через единственный глобальный параметр – суммарную одноэлектронную плотность, что и отражено в названии метода. Данный метод дает наилучший компромисс между достигаемой точностью расчетов и размерами изучаемых систем. Вычислительные затраты растут с увеличением размера расчетной ячейки как ~N ³; хотя для некоторых задач возможен и более слабый рост ~ N. В лучших мировых компьютерных центрах данный метод позволяет проводить расчеты на ячейках, содержащих до тысячи атомов. Поэтому в наши дни DFT является активно используемым рабочим инструментом для исследований в физике дефектов в металлах и полупроводниках.

• Метод сильной связи (англ. Tight Binding или TB). Метод основан на тех же общих принципах, что и метод Хартри-Фока, но при этом часть членов в квантово-механическом операторе энергии (операторе Гамильтона или просто гамильтониане) заменены приближенными или полностью опущены. Кроме того, точные волновые функции электронов заменяются некоторой совокупностью приближенных. Соответственно, существует довольно много вариаций метода, различающихся уровнем используемых упрощений. В самых простых моделях TB даже кулоновское отталкивание электронов принимается во внимание в опосредованном виде. Для того, чтобы скомпенсировать ошибки, появляющиеся в результате отсутствия в гамильтониане некоторых членов, в другие части вводятся подгоночные коэффициенты, чтобы обеспечить максимально возможное согласие с экспериментальными данными или результатами расчетов методами DFT или Хартри-Фока. Вычислительные затраты метода растут, как и в методе DFT, ~N ³, но в силу более простых уравнений позволяют рассчитывать системы содержащие по меньшей мере на порядок больше атомов, чем DFT. Однако и надежность оценок, получаемых с использованием этого метода, заметно ниже. Важной особенностью метода является возможность вычислить, в определенных приближениях, взаимодействие между атомами в аналитическом виде, что иногда используется для создания эмпирических потенциалов. В частности, эмпирические потенциалы класса Абеля-Терсоффа могут быть строго выведены как некоторое приближение метода сильной связи.

Рассмотрим, в общих чертах, какие именно приближения позволяют превратить квантово-механическое описание поведения электронов в практически реализуемую задачу. Как известно из квантовой механики, система, состоящая из некоторого числа ионов и электронов, описывается некоторой комплексной функцией от координат всех имеющихся в системе частиц, называемой волновой функцией. Квадрат модуля волновой функции определяет вероятность нахождения частиц в определенных положениях. Волновая функция удовлетворяет, в простейшем случае, стационарному уравнению Шредингера:

, (14.1)

где - оператор Гамильтона и - полная энергия системы. Оператор Гамильтона можно представить в виде:

, (14.2)

где и - дифференциальные операторы кинетической энергии отдельно для систем ионов и электронов, - потенциал взаимодействия ионов и электронов, а и - потенциалы, соответственно, электрон-электронного и ион-ионного взаимодействия. Хотя уравнение Шредингера записывается в относительно компактной форме, его точное решение в материаловедческих задачах не представляется возможным из-за слишком большого числа частиц, заключенных даже в относительно малых (нанометрических) объемах материала. Кроме того, поскольку электроны и ионы – заряженные частицы, взаимодействующие друг с другом посредством дальнодействующего Кулоновского потенциала, движение каждого отдельно взятого электрона или иона зависит от движения всех остальных частиц. В результате, точный расчет системы такой ошеломляющей сложности лежит далеко за пределами возможностей самых мощных современных компьютеров. Поэтому квантово-механические подходы используют ряд приближений, позволяющих сохранить основные свойства электронного и атомного взаимодействия.

Приближение Борна-Оппенгеймера. Одним из наиболее важных приближений в квантово-механических вычислительных методах является приближение Борна-Оппенгеймера. Оно исходит из того, что ионы на несколько порядков величины тяжелее электронов и, при одной и той же температуре, движутся значительно медленнее. В результате, можно с хорошей точностью считать, что распределение электронов в материале адиабатически подстраивается к текущим положениям ионов. Если обозначить вектор положения отдельного иона как R _I, а полную совокупность всех положений ионов как { R _I }, то полную волновую функцию в приближении Борна-Оппенгеймера можно представить в виде прямого произведения волновых функций электронов, , и атомных ядер, c,

, (14.3)

где электронная волновая функция зависит не только от положений электронов { r _i }, но и параметрически – от положений ионов. Подобное разбиение позволяет записать уравнения Шредингера отдельно для электронов и ионов, причем поведение ионной подсистемы, за исключением самых легких химических элементов, обычно достаточно рассматривать в квазиклассическом или просто классическом приближении. На практике приближение Борна-Оппенгеймера позволяет реализовать численную схему, полностью аналогичную эмпирическим методам: ионы двигаются согласно собственным уравнениям движения, а взаимодействие между ними описываются путем решения квантово-механического уравнения для электронов, в котором позиции ионов фиксированы.

Следует, однако, иметь в виду, что встречаются ситуации, когда корреляции между ионным и электронным движением существенны и приближение Борна-Оппенгеймера неприменимо. Реалистичным примером такой ситуации является движение через твердое тело ионов, ускоренных до энергий в сотни МэВ.

Одноэлектронное приближение. Хотя исключение ионов из игры с помощью приближения Борна-Оппенгеймера является важным шагом вперед, получающееся при этом уравнение для электронов по-прежнему остается многочастичным. Строго говоря, с этой точки зрения достигаемый выигрыш не особенно существенен, поскольку электронов в материалах значительно больше чем ионов. Однако теперь уравнение записывается только для электронов и можно ввести принципиальное допущение о возможности описания каждого отдельного электрона с помощью его собственной одноэлектронной волновой функции (орбитали), независимой от других электронов в системе. Во всех углубленных курсах квантовой механики подчеркивается, что подобное допущение заранее ниоткуда не следует и его строгое обоснование действительно совершенно неочевидно, но великолепные практические результаты использования этого приближения в физике твердого тела являются серьезным аргументов пользу его оправданности. В результате использования одноэлектронного приближения, единое уравнения Шредингера для многочастичной волновой функции сводится к системе уравнений для каждого отдельного электрона. А поскольку, согласно одному из основных постулатов квантовой механики электроны принципиально неразличимы, то при некоторых дополнительных упрощениях полученную систему уравнений можно свести к задаче об определении собственных значений и собственных функций для одного единственного одноэлектронного уравнения. Именно эта процедура и реализована в методе DFT, что и определяет его популярность, поскольку для решения задач на собственные значения разработаны эффективные методы численного решения.

Теория функционала электронной плотности. Исторически, предпосылками создания теории функционала электронной плотности является предложенный в 1956г. Слэтером упрощенный вариант теории Хартри-Фока, в котором наиболее сложные для практических расчетов члены в одноэлектронных уравнениях заменены на приближенные, зависящие только от волновой функции рассматриваемого электрона и от интегрального описания влияния всех прочих электронов. При этом, полученный приближенный интеграл оказался параметрически зависящим только от суммы одноэлектронных плотностей всех электронов. Этот результат натолкнул в начале 1960-х годов американского ученого Кона (W. Kohn) с соавторами на мысль о том, что знания суммы одноэлектронных плотностей (полной электронной плотности), в принципе, достаточно для того, чтобы однозначно описать все одночастичные волновые функции многоэлектронной системы (теорема Хоненберга-Кона). В результате, в 1964 году Хоненберг и Кон и в 1965 году Кон и Шэм предложили радикальное изменение предложенного Слэтером приближенного одноэлектронного уравнения, формально дополнив членом, параметрически учитывающим все эффекты, необходимые для адекватного описания электрон-электронного вазимодействия. Более того, они постулировали, что этот дополнительный член (так называемый обменно-корреляционный интеграл) может быть однозначно выражен в виде некоторого функционала полной электронной плотности. Полученные в результате уравнения принято называть уравнениями Кона-Шема. Хотя никаких строгих рекомендаций по выбору этого функционала плотности теория не дает, да и само по себе математическое понятие функционала не означает возможности представления искомого интеграла в виде аналитической функции от полной электронной плотности, на практике, методом проб и ошибок, удалось подобрать такие приближенные выражения для обменно-корреляционного члена, которые достаточны для эффективного описания поведения расчетных систем на атомистическом уровне. Стоит упомянуть, что в процессе подбора широко и эффективно использовался описанный в разделе 14.2.2 метод использования предельных случаев для оценки поведения развиваемой математической модели.

Исторически первое приближение для обменно-корреляционной энергии, называемое приближением локальной плотности (англ. local density approximation или LDA) было предложено в упоминавшихся работах Слетера и, в усовершенствованном виде, Кона с соатворами. Оно оказалось в вычислительном отношении достаточно удобным и на удивление точным. В этом приближении считается, что электрон в произвольной пространственной точке демонстрирует тот же самый отклик на коллективное воздействие со стороны окружающих электронов, как и в случае, когда плотность электронов по всему пространству постоянна и имеет ту же величину, что и в точке, где находится рассматриваемый электрон. Тогда плотность обменно-корреляционной энергии может быть оценена из известных результатов для электронной системы с постоянной плотностью (однородного электронного газа), а обменно-корреляционная энергия всего твердого тела является интегралом по вкладам от каждого элемента объема. Метод LDA точен для идеального металла в так называемом приближении «желе» (когда все положительные заряды ионов равномерно размазаны по объему материала, а электронная плотность постоянна) и становится менее точным для реальных систем с переменной электронной плотностью.

Блок-схема применения DFT алгоритма для расчета одноэлектронных орбиталей дана на рис. 14.3. После того, как все орбитали и собственные значения определены, их можно использовать для определения полной энергии и любых других наблюдаемых величин, используя квантовомеханические средние величины соответствующих операторов.

Рис. 14.3.. Блок-схема алгоритма DFT для расчета одноэлектронных орбиталей.

Псевдопотенциалы и расширенные плоские волны. Строго говоря, даже после всех предположений, полное численное решение уравнений Кона-Шема, хотя принципиально и возможно, требует запредельных вычислительных ресурсов. Поэтому для численного нахождения одноэлектронных орбиталей вводят дополнительные упрощения. Обсудим некоторые наиболее важные из них.

Для описания всех одноэлектронных орбиталей в системе содержащей N электронов необходимо определить как минимум N собственных функций уравнения Кона-Шема, отвечающих первым N собственным значениям энергии (по возрастанию, начиная с наименьшего). Полное число электронов в системе однозначно задается числом и типом атомов рассматриваемой системы, однако, с практической точки зрения, интерес представляют далеко не все электроны. Как известно из курсов химии и атомной физики, для не слишком легких элементов большинство электронов в атоме довольно прочно связано с ионом, тогда как в формировании химической связи принимает участие сравнительно небольшое число наиболее слабо связанных с атомом (так называемых валентных) электронов. Поэтому часто представляется разумным решать уравнения Кона-Шема только для валентных электронов, а ион вместе с сильно связанными с ним электронами рассматривать как некоторое единое ядро (англ. core), в котором пространственное распределение электронов определяется в основном кулоновским взаимодействием электронов с ионом и между собой. Поскольку определяющим в области ядра является сильное кулоновское взаимодействие электронов с ионом, можно ожидать, что волновые функции электронов будут близки к электронным орбиталям в изолированном атоме. В курсе атомной физики показывается, что состояния электронов в атоме квантуются и соответствующие электронные орбитали для разных квантовых чисел достигают максимума на разных расстояниях от иона. В результате, полная электронная плотность в пределах ядра является быстро осциллирующей функцией расстояния от иона. Это создает серьезные проблемы для численного определения волновых функций валентных электронов.

Стандартным методом решения уравнения Кона-Шема, представляющего собой дифференциальное уравнение второго порядка, является разложение искомых функции в ряд по некоторому полному набору базисных функций, что позволяет свести дифференциальное уравнение для функции к системе алгебраических уравнений для коэффициентов разложения. Очевидно, что для описания системы из N электронов необходимо использовать как минимум N независимых базисных функций, хотя в реальности число базисных функций (и соответственно – коэффициентов разложения) значительно больше N и в пределе стремится к бесконечности. Поскольку решение бесконечной системы алгебраических уравнений в общем случае невозможно, в разложении ограничиваются конечным числом членов разложения, что приводит к погрешности в определении одноэлектронных орбиталей. Чтобы повысить эффективность расчетов, желательно использовать такой набор базисных функций, который позволил бы ограничиться как можно меньшим их количеством, не снижая точности расчета ниже некоторой наперед заданной погрешности.

Как показано схематически на рисунке 14.4, в областях вне атомных ядер изменение электрического потенциала, создаваемого экранированными ионами, сравнительно плавное и волновые функций валентных электронов в этой области достаточно хорошо описываются ограниченным набором базисных функций. Однако в области ядер распределение заряда, а значит и волновая функция валентного электрона. При достаточно часто используемом разложении валентных орбиталей в ряд Фурье по плоским волнам это означает необходимость учета очень большого числа высокочастотных гармоник. Это сильно усложняет расчет энергии и сил взаимодействия между атомами, не приводя к улучшению его точности, поскольку химическая связь между атомами обеспечивается распределением электронов в области вне атомных ядер, где высокочастотные гармоники взаимно компенсируются.

Рис.14.4. Схематическое изображение электронного (сплошные линии) и псевдоэлектронного (пунктирные линии) потенциала и соответствующих волновых функций. Расстояние, начиная с которого потенциалы совпадают, обозначено через r c

Для того, чтобы обойти проблему быстрых колебаний, на практике используется два основных приема:

(i) Метод псевдопотенциала. В этом подходе сильно осциллирующий самосогласованный электрический потенциал около ядер приближенно заменяется плавно меняющимся (" мягким") псевдопотенциалом, после чего разложение волновых функций по плоским волнам во всем пространстве не представляет особых проблем. Детальная процедура построения псевдопотенциалов является довольно сложной и представляет собой самостоятельный раздел исследований, широко рассматриваемый в специальной литературе.

Помимо чисто расчетного выигрыша, использование псевдопотенциалов позволяет избежать ряд существенных технических проблем, возникающих при использовании для описания ядер полного кулоновского потенциала. Прежде всего, в практических расчетах интерес представляет, как правило, разница в энергиях между сравнительно близкими конфигурациями пространственного расположения атомов. Для атомов с большим числом электронов полная энергия оказывается чрезвычайно большой, что может приводить к существенной потере точности. Во-вторых, аппроксимация волновых функций ядра чрезвычайно сложна, а сравнительно небольшие ошибки могут приводить к существенным различиям в собственных значениях энергии для сильно-связанных электронов. Псевдо-волновая функция является намного более простой для аппроксимации и более гладкой функцией, чем полноэлектронная волновая функция. В-третьих, для более тяжелых атомов важны релятивистские эффекты, и для электронов вблизи ядра требуется использовать уравнение Дирака. Однако валентные электроны по-прежнему могут рассматриваться, как не-релятивистские и можно ввести спин-орбитальный потенциал, который описывает поляризованные валентные электроны.

(i) Метод расширенных плоских волн (англ. plane augmented wave или PAW). Этот подход отказывается от попытки решать уравнение Шредингера вблизи атома путем разложения в ряд Фурье, вместо чего непосредственно решает его в прямом пространстве для разных энергий валентных электронов. При этом область ядра считается сферой, внутри которой потенциал полагается сферически симметричным, а снаружи - постоянным (обычно равным нулю). В англоязычной литературе такое приближение называется “muffin-tin” (по названию формы для выпекания бисквитов, на которую похож получающийся потенциал). После этого можно искать решения для волновых функций валентных электронов с помощью разложения по плоским волнам только в областях вне атомных ядер, дополнительно требуя, чтобы на границах атомных ядер эти решения непрерывно переходили во «внутренние» функции для той же энергии (непрерывности производных, как правило, не требуется).

Поверхность потенциальной энергии и расчет сил, действующих на ионы. Часто наиболее практически важными величинами, определяемыми в численных экспериментах на атомарном уровне, являются полная энергия исследуемой системы и силы действующие на ионы. Как мы помним, моментальные положения ионов являются параметрами уравнения Шредингера для электронов, так что энергия электронной подсистемы E_e является функцией координат ионов. Соответственно и полная энергия изучаемой системы в приближении Борн-Оппенгеймера, E^BO, напрямую зависит от конкретного расположения ионов,

, (14.4)

где сумма, описывающая кулоновское взаимодействие ионов, берется по всем возможным парам ионов, Z_I - заряд иона I, и R_IJ – расстояние между ионами I и J.

Удобно рассматривать потенциальную энергию Борна-Оппенгеймера как многомерную поверхность в пространстве положений ионов. По определению, локальные минимумы на потенциальной поверхности соответствуют метастабильным конфигурациям, абсолютный минимум - самой устойчивой (стабильной) конфигурации. Весьма часто главной целью атомистического моделирования является именно оптимизация геометрии системы, то есть нахождение таких положений ионов, при которых реализуется локальный или глобальный минимум энергии. Процедуру, используемую для поиска минимума, называют алгоритмом оптимизации. Примеры существующих алгоритмов минимизации энергии будут рассмотрены ниже в разделе 14.3.1.3.

При исследовании динамического поведения ионов, а также в ряде наиболее эффективных алгоритмов минимизации энергии необходимо иметь информацию о силах, действующих на ионы. По общему правилу, силу 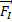, действующую на ион I, представляет собой взятый с обратным знаком градиент полной энергии системы относительно положения этого иона,

. (14.5)

Когда энергия задана как аналитическая функция ионных координат, ее вычисление не представляет особого труда. Однако при квантово-механическом расчете определяется только полная энергия системы. Строго говоря, и вычисляя только энергию возможно численно оценить силы на отдельные ионы, если придавать каждому иону малые смещения в разных направлениях. Однако для системы, состоящей из N ионов, это требует 6 N независимых расчетов энергии, что практически нереально с точки зрения вычислительных ресурсов. К счастью, в действительности силу, действующую на любой ион, можно вычислить непосредственно как квантово-механическое среднее от оператора, представляющего собой частную производную от оператора Гамильтона по координатам этого иона, . Для вычисления такого среднего достаточно знания тех же одноэлектронных волновых функций, которые используются для расчета полной энергии системы. Строгое математическое доказательство этого замечательного результата носит название теоремы Хеллмана-Фейнмана.

Теорема Хеллмана-Фейнмана сильно упрощает расчеты с практической точки зрения. Действительно, в этом случае весьма затратная в вычислительном отношении задача нахождения собственных значений и собственных функций электронного квантово-механического уравнения решается для заданного расположения ионов только единожды, а затем силы вычисляются, используя матрицу производных гамильтониана, вычисленную аналитически и сохраненную в памяти компьютера. Следует однако иметь в виду, что силы вычисленные с помощью теоремы Хеллмана-Фейнмана очень чувствительны к ошибкам в волновых функциях, поскольку погрешность вычисления сил того же порядка, что и погрешность волновых функций. Достаточно точно силы могут быть вычислены только, когда волновая функция очень близка к точному собственному состоянию. Погрешность вычисления энергии - второго порядка относительно ошибок в волновых функциях, так что значительно легче точно вычислить полную энергию, чем точно вычислить силы на ионы.