Автомодельные решения модели нелинейной теплопроводности

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Исследование поведения сложных систем, модели которых описываются нелинейными уравнениями, в ряде случаев эффективно с помощью автомодельных решений этих уравнений. Автомодельными решениями называются такие решения нелинейного дифференциального уравнения (системы уравнений), конкретный вид которых определяется путем интегрирования некоторых обыкновенных дифференциальных уравнений. Автомодельные решения являются, как правило, теми решениями (аттракторами), к которым асимптотически приближаются все остальные решения данного уравнения (системы уравнений). Существование у рассматриваемой нелинейной модели автомодельного решения существенно упрощает ее исследование. Для примера рассмотрим уравнение теплопроводности (14.69) с коэффициентом теплопроводности, зависящим от температуры λ (T) = λ ₀ T ^s. Зададим температуру на границе х = 0 степенным образом зависящей от времени (нагрев лазерным излучением поверхности):

Положим также: T (x, 0 ) = 0, при x ³ 0. Данная задача (14.69), (14.71) допускает автомодельное решение следующего вида:

где функция f(z) определяется из обыкновенного дифференциального уравнения, получающегося после подстановки выражения (14.72) в уравнение (14.8):

Функция f (z) должна также удовлетворять краевым условиям:

Поскольку уравнение (14.8) является вырождающимся и допускает конечную скорость распространения возмущений, необходимо дополнительно потребовать непрерывности теплового потока f ^s ·∂ /f∂ z. При m ≠ 1/s задачу можно решить только численно (в случае m = 1/s решение в точности совпадает с бегущей волной (14.70)). С помощью замены:

уравнение (14.73) сводится к автономному виду и допускает понижение порядка. В новых переменных (14.75) можно провести анализ его решений на фазовой плоскости и определить его основные свойства. При любых значениях параметра m > 0 функция f(z) является финитной т. е. существует такое z ₀ = z ₀(m, s) > 0, что f (z)º 0 для всех z ³ z ₀ и f (z) > 0 при 0 £ z £ z ₀. Поэтому решение (14.72) также финитно по х и представляет собой тепловую волну, движущуюся по невозмущенному фону температуры. Из выражения (14.72) для переменной z следует, что положение точки фронта «волны» х _ф(t), характеризующееся равенством z = z ₀, определяется в каждый момент времени по формуле:

т. е. тепловая волна ускоряет со временем свое движение и в пределе при t ® + ¥ нагревает до бесконечно больших температур все пространство х ³ 0. Данное автомодельное решение является асимптотически устойчивым относительно малых возмущений граничных условий и отклонений коэффициента теплопроводности от степенной зависимости. Так как в реальных физических процессах бесконечные температуры не достигаются, то об автомодельном решении (14.72) можно говорить как о промежуточной асимптотике моделируемого процесса нагрева, которая реализуется при не слишком малых и не очень больших временах.

Меняя граничные условия для уравнения (14.69), можно получить новый класс автомодельных решений, обладающих рядом отличительных особенностей.

Зададим изменение температуры на границе х = 0 в режиме с обострением:

T (0, t) = T ₀ (t ₀ – t) ⁿ, 0 £ t < t ₀; t ₀ =const > 0. (14.77)

Постоянная n < 0, поэтому T (0, t)® + ¥ при t ® t ₀. Режимом с обострением называется такой закон изменения некоторой величины, который обеспечивает ее неограниченное возрастание в течение конечного времени (в данном случае равного t ₀). Режимы с обострением, аналогичные (14.77), используются при описании существенно нестационарных физических процессов (лазерного и ионно-плазменного воздействия на поверхность материалов). Таким специфическим граничным условиям отвечают решения с весьма необычными свойствами. Уравнение (14.69) с граничными условиями (14.16) имеет автомодельное решение:

Задача (14.79) решается аналогично задаче (14.73), (14.74) с помощью замены (14.75) сведением к уравнению первого порядка и последующим анализом поля интегральных кривых. Свойства решения задачи (14.79) и самого автомодельного решения (14.78) существенно зависят от соотношения между величинами n и s. Если n < - 1/s, то функция f (z) имеет конечный носитель длины z ₀ = z ₀(n, s) < +¥. В случае n > - 1/sрешение задачи (14.79) строго положительно для любых z > 0 и является бесконечно дифференцируемой функцией. Наиболее простым является случай n = - 1/s, при котором решение задачи (14.79) записывается в явном виде:

Автомодельное решение (14.78) для случая n = - 1/s с учетом выражения (14.80) представляет собой весьма необычную тепловую волну с остановившимся фронтом (впервые получено А.А. Самарским и И.М. Соболем в 1963 г.):

Из (14.82) следует, что тепло вообще не проникает далее глубины х = х ₀, несмотря на неограниченный рост температуры на границе х = 0 и во всех внутренних точках интервала 0 £ х £ х ₀. Решение (14.82) наглядно проявляет свойство локализации тепла, которое в данном случае характеризуется тем, что в пространстве образуется область с отличной от нуля температурой, не изменяющая своих размеров в течение конечного времени. Внутри области локализации температура и количество поступающей энергии возрастают при t ® t ₀. Величина х ₀ называется глубиной локализации. В общем случае локализованным называют такое решение, которое неограниченно возрастает в течение конечного времени в ограниченной части пространства. Заметим, что ранее рассматривавшиеся автомодельные решения таким свойством не обладали.

Задача о фазовом переходе. Задача Стефана. При изменении температуры конденсированной среды может происходить изменение его физического состояния, в частности, при переходе температуры через точку плавления – переход из жидкой фазы в твердую (или обратный переход). На поверхности фазового перехода сохраняется постоянная температура. При движении поверхности фазового перехода происходит выделение (поглощение) скрытой теплоты плавления. На границе раздела фаз должно выполняться условие теплового баланса. Рассмотрим плоскую задачу, когда границей раздела является плоскость х = x(t), на которой выполняется условие (х₁ = x = х₂):

где u ₁, u ₂ – температуры, λ ₁, λ ₂ – коэффициенты теплопроводности первой и второй фаз соответственно, а L _пл - скрытая теплота плавления. Это условие имеет место как для процесса затвердевания (кристаллизации): d x /dt > 0, так и для процесса плавления: d x /dt < 0, направление процесса определяется знаком левой части условия (14.83).

В качестве примера рассмотрим процесс замерзания воды, при котором температура фазового перехода равна нулю. Рассматриваем массу воды х ³ 0. В начальный момент t = 0 вода имеет постоянную температуру T ₀ > 0. На поверхности воды х = 0 поддерживается постоянная температура T _* = 0, граница промерзания х = x со временем проникает вглубь жидкости. Задача о распределении температуры при наличии фазового перехода и о скорости движения границы раздела фаз сводится к решению уравнений:

где λ ₁, a ₁² и λ ₂, a ₂² – коэффициенты теплопроводности и температуропроводности соответственно твердой и жидкой фаз. Задачу (14.84)–(14.87) называют задачей Стефана, задачей о фазовом переходе или задачей о промерзании. Ее решение имеет вид

где А ₁, B ₁, A ₂, B ₂ – пока неопределенные постоянные, а Ф – интеграл ошибок:

Так как эти условия должны выполняться при любых значениях времени, что возможно только при

где α - некоторая постоянная. Соотношение (14.89) определяет закон движения фазовой границы.

Для постоянных А ₁, B ₁, A ₂, B ₂ получаются выражения:

Постоянная α определяется из соотношения (14.87):

Решение этого трансцендентного уравнения и дает значение α. Существование хотя бы одного решения при T _* < 0, T ₀ > 0 следует из того, что при изменении α от 0 до + ¥ левая часть уравнения изменяется от – ¥ до + ¥, а правая от 0 до – ¥. Для случая T ₀ равно температуре плавления T ₀ = 0, выражения (14.90), (14.91) упрощаются:

приведенным на рис. 14.7, легко графически определить значение α.

Решение задачи Стефана может быть получено при помощи метода подобия. Эту задачу можно решать также для тех случаев, когда скрытая теплота плавления выделяется не при фиксированной температуре, а в некотором интервале температур. Подобный метод решения используется и для задачи, если имеется несколько критических температур, что встречается при фазовых превращениях в процессе перехода от одной кристаллической структуры к другой, например, при перекристаллизации стали. Наиболее эффективным методом численного решения задач о фазовых переходах является метод конечных разностей, который применим для случаев двух и трех пространственных переменных при наличии нескольких фазовых переходов.

Компьютерное моделирование воздействия на поверхность материала мощным ионным пучком. Рассмотрим компьютерное моделирование на основе задачи Стефана реального технологического процесса обработки поверхности композиционного материала мощным ионным пучком.

Воздействие пучков заряженных частиц высоких плотностей энергии приводит к образованию в приповерхностных слоях материалов сильно неравновесных структурно-фазовых состояний, оказывающих положительное влияние на свойства металлов и сплавов. С этим связаны определенные перспективы использования мощных ионных пучков в технологических целях. Вместе с тем механизмы формирования поверхностных структур в композиционных материалах, обусловленные главным образом термическими и термомеханическими эффектами, являются малоизученными. Соответственно, остаются нерешенными и вопросы управления поверхностными свойствами материалов путем ионно-лучевой модификации. Данная компьютерная модель позволяет численно исследовать инициируемые воздействием мощных ионных пучков термические процессы в приповерхностных слоях композиционного материала (сплава системы WC-Co) с целью конкретизации механизмов формирования экспериментально зафиксированных поверхностных структур и оценке применимости используемых расчетных методов для объяснения полученных экспериментальных данных.

Постановка и алгоритм решения задачи. При принятых предположениях, задача определения пространственно-временного распределения поля температур T (x, t), обусловленного радиационным разогревом, сводится к решению одномерного нелинейного уравнения теплопроводности с переменными коэффициентами

Здесь ρ - плотность облучаемого материала; c (T), λ (T) - теплоемкость и теплопроводность соответственно, зависящие от температуры; T ₀ - начальная температура облучаемого образца; l - координата его задней поверхности. На границе раздела фаз «жидкость - твердое тело» должно обеспечиваться условие равенства потоков тепла с учетом его потерь на фазовые превращения:

где q_m - удельная теплота плавления материала; λ (T_m) - коэффициент теплопроводности при температуре плавления; x_m - координата границы раздела жидкой и твердой фаз; W (x_m, t) - поток энергии через границу раздела фаз, обусловленный энерговыделением тормозящихся ионов. На поверхности образца должно выполняться еще одно условие, обеспечивающее баланс энергии с учетом испарения:

где q _e - удельная теплота испарения; λ (T _e) -коэффициент теплопроводности при температуре кипения; x _e - координата испаряющейся поверхности в произвольный момент времени (x_e = 0 при t = 0); W (x _e, t) - поток энергии через поверхность, обусловленный налетающими ионами. Задача (14.92)-(14.96) решается численными методами. Используя преобразование Кирхгофа

где S (T) - характеристическая, " безразмерная" температура, нелинейное уравнение (14.31) приводится к виду:

где a (S) - коэффициент температуропроводности, зависящий от температуры S и вычисляемый в общем случае по формуле:

Уравнение (14.98) решалось по неявным схемам с квазиравномерной сеткой. Теплофизические характеристики среды λ (T) и c (T) аппроксимировались кусочно-непрерывными линейными функциями температуры. В этом случае переход от характеристической температуры S к реальной Т осуществляется по формуле:

Здесь λ ₀ и λ ₀^’ - значения коэффициента теплопроводности и его производной при начальной температуре T ₀. Процессы плавления и испарения моделируются методом ячеек.

Анализ и сопоставление результатов моделирования. Расчеты тепловых полей проводились для материала ВК8 при воздействии мощным ионным пучком состава (30% протонов + 70% ионов углерода) со средней энергией 300 кэВ и длительностью импульса 50 нс. Функция источника F (x, t) из формулы (14.31) представлялась в виде:

где: J _max - плотность тока пучка при его максимальном значении; e - заряд электрона (ионы однократно ионизированы); j (t) - временное распределение плотности тока в импульсе; f (x) - пространственное распределение потерь энергии одним ионом. Для пучка смешанного состава f (x) представлялась как сумма вкладов различных компонент:

где f _C(x) -профиль энерговыделения ионов углерода; f _H(x) - ионов водорода; C _C и C _H - их доли в пучке.

Основные результаты численного моделирования с постоянными теплофизическими характеристиками для твердого сплава ВК8 представлены на рис. 14.6 – 14.10.

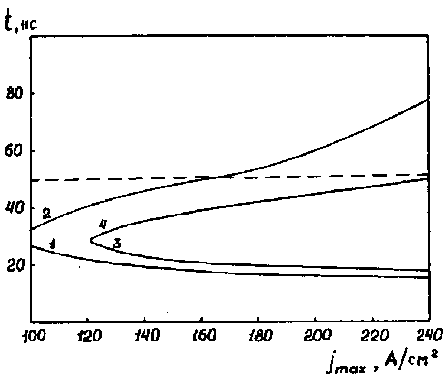
Рис. 14.8. Зависимость времен начала и окончания плавления (кривые 1, 2), начала и окончания испарения (кривые 3, 4) от максимальной плотности тока при облучении образца из твердого сплава ВК8. Пунктирная прямая - длительность импульса

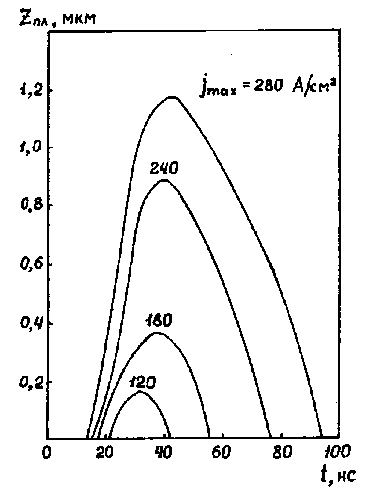
Рис. 14.9. Зависимость глубины проплавленного слоя от времени для указанных значений максимальной плотности тока; глубина отсчитывается от передней поверхности необлученного образца

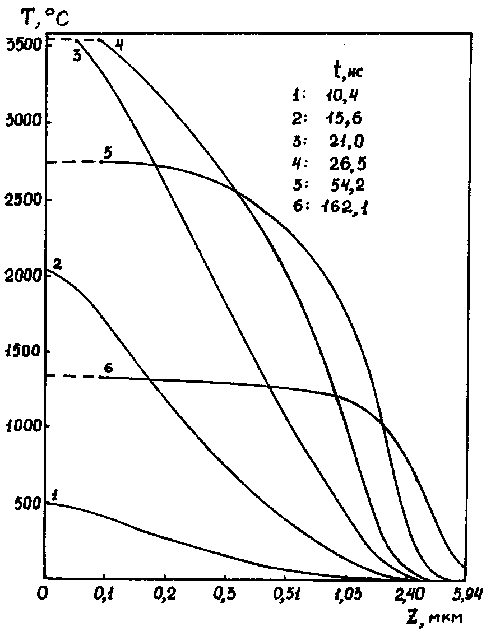
Рис. 14.10. Зависимость температуры от глубины мишени в указанные моменты времени. Пунктиром отмечено текущее состояние передней поверхности. Температура отсчитывается от комнатной; расчет сделан для j _max = 180 А/см²

На рис. 14.8 видно, что испарение имеет место, начиная приблизительно с J _max = 120 А/см². Если испарение прекращается еще до окончания импульса, то плавление мишени может продолжаться и после окончания воздействия импульсным пучком. Это обусловлено так называемым " перегревом" той области мишени, где происходило энерговыделение. Расчеты с зависящими от температуры теплофизическими характеристиками материала приводят к следующим отличиям от результатов с постоянными коэффициентами:

а) увеличивается время достижения температур плавления и кипения и минимальная плотность тока ионного пучка, при которой в мишени начинаются процессы плавления и испарения (последнее, например, происходит лишь при J _max > 130 А/см²);

б) уменьшаются максимальная температура на поверхности образца для одних и тех же плотностей тока, время начала процесса кристаллизации, максимальные глубины slush-зоны, зоны проплавления и толщина испарившегося слоя, максимальный градиент температуры и скорость изменения температуры в образце.