Фракталы и фрактальные структуры

Теоретическая физика твердого тела в основном рассматривала равновесные системы. Необратимые процессы рассматривались только весьма упрощенным способом — как малые возмущения, например, при изучении транспортных явлений. Известно, что конденсированное состояние вещества может существовать не только в форме плотной сплошной среды, но и в виде сильно разрыхленных пористых структур. Такого рода структуры образуются, как правило, в результате конденсации в сложных неравновесных условиях, например, при слипании движущихся по определенному закону твердых частиц или в результате взаимодействия дислокаций при пластической деформации металлов. Подобного рода структуры получили название фрактальных агрегатов. Они в большинстве своем являются неупорядоченными, сложными для исследования, и их макроскопические свойства мало изучены. Фрактальный агрегат каждого вещества формируется при определенных физических условиях, которые до конца не поняты. Тем не менее то, что уже известно, дает возможность использовать законы образования фрактальных агрегатов для создания материалов с необычными физическими свойствами. Фрактальные твердотельные среды, сформированные в условиях диссипации энергии в открытых системах и являющиеся самоорганизованными структурами, обладают рядом необычных свойств, которые невозможно получить при традиционных способах формирования структурного состояния вещества. Движущей силой самоорганизации в диссипативных системах является стремление вещества в открытых системах к снижению энтропии. Характерные признаки фрактальных структур – самоподобие, масштабная инвариантность, структурная иерархия, пористость нанометрового масштаба и фрактальная размерность.

Твердотельные фрактальные системы представляют собой новый тип структурного состояния вещества, характеризующегося уникальными физическими свойствами. Фрактальные твердотельные системы образуются из атомов или молекул, а также из наноразмерных частиц или кластеров. Сформированные из таких частиц или кластеров фрактальные микро- или макроскопичские структуры интересны как для изучения фундаментальных свойств, так и для использования в новых технологиях. Экспериментально установлено, что фрактальная структура, сформированная из наночастиц металлов, способна поглощать электромагнитное излучение в световом диапазоне длин волн. Показано, что термоэдс фрактальной структуры углерода увеличивается почти на порядок по сравнению с графитом.

Во многих случаях фрактальная структура твердого тела обеспечивает высокие удельные прочностные характеристики, низкую теплопроводность и звукопроницаемость. Поэтому получение и исследование веществ, имеющих определенную фрактальную структуру, является актуальной задачей. Характерная особенность фрактальных образований состоит в том, что их структура проявляется только при совместном разрешении нескольких уровней, разница масштабов которых затрудняет представление наглядного геометрического образа (типа изрезанной береговой линии).

Хотя наблюдение самих многомасштабных структур затруднительно, их последовательное описание может быть достигнуто только в рамках фрактальной идеологии. Это связано с тем, что такие неравновесные системы представляются как суперансамбли, состоящие из иерархически соподчиненных статистических ансамблей, которые, в свою очередь, состоят из набора подансамблей и т.д. Поэтому, говоря о фракталах в конденсированной среде, следует иметь в виду, прежде всего, использование концепции, а не буквальное описание наблюдаемого геометрического образа.

Одной из важнейших характеристик фрактальных структур, определяющей их физические свойства, является фрактальная размерность.

Математическое определение фрактальной размерности. Объем фрактала в своем пространстве вложения всегда равен нулю. Он, однако, может быть отличен от нуля в пространстве меньшей размерности. Чтобы определить размерность этого пространства D, разобьем все n -мерное пространство на малые кубики с длиной ребра ε и объемом ε n (рис. 14.12).

Рис. 14.12 Определение фрактальной размерности

Пусть N (ε) — минимальное число кубиков, которые в совокупности полностью покрывают фрактальное множество, тогда по определению

. (14.103)

Эту величину обычно называют хаусдорфовой или фрактальной размерностью.

Существование этого предела означает конечность объема фрактала в D -мерном пространстве при малом ε:

N (ε)≈ V ε ^{– D} , (14.104)

где V = const.

Таким образом, N (ε) есть не что иное, как число D -мерных кубиков, покрывающих в D -мерном пространстве объем V, поскольку покрывающие фрактал n -мерные кубики могут оказаться почти пустыми

D < n, (14.105)

и в отличие от привычной размерности D может быть дробной величиной, каковой она чаще всего и является для фрактальных множеств. Очевидно, что для обычных множеств это определение приводит к хорошо известным результатам. Так, для множества N изолированных точек имеем N (ε) = N и поэтому

. (14.106)

Для отрезка достаточно гладкой линии длины L N (ε) = L /ε и поэтому D = 1. Для площадки S двумерной поверхности N (ε) = S /ε ² и D = 2 и т.д.

Первоначально фрактал был введен как геометрический объект в обычном физическом пространстве. Поэтому целесообразно начать рассмотрение примеров фракталов с наглядных геометрических построений Кантора и Коха. Их выбор обусловлен тем, что в первом случае фрактальная размерность D меньше топологической d, а во втором D > d.

Канторовское множество. Возьмем отрезок длины 1. Разделив его на три равные части, исключим среднюю часть. С оставшимися двумя отрезками проделаем ту же процедуру и в результате получим 4 отрезка в 1/9 длины каждый и т.д. до бесконечности (рис. 14.13).

Рис. 14.13. Построение канторовского множества

Множество точек, возникшее после этой процедуры, и является канторовским множеством. Нетрудно заметить, что длина L этого множества равна нулю. Действительно,

. (14.107)

Найдем теперь его хаусдорфову или фрактальную размерность. Для этого выберем в качестве " эталона" отрезок длиной

. (14.108)

Минимальное число таких отрезков, необходимых для покрытия множества, равно

N (ε) = 2 ⁿ. (14.109)

Поэтому его фрактальная размерность

. (14.110)

Снежинка Коха. Пример построения этого фрактала изображен ниже на рис. 14.14

Рис. 14.14 Снежинка Коха

Снежинка Коха представляет собой линию бесконечной длины, ограничивающую конечную площадь. Первое утверждение доказывается очень просто. Если мы заметим, что при каждом шаге число сторон многоугольника увеличивается в 4 раза, а длина каждой стороны уменьшается только в 3 раза. Если принять длину стороны образующего треугольника за 1, то тогда длина снежинки Коха:

. (14.111)

Площадь под кривой, если принять площадь образующего треугольника за 1, равна

(14.112)

Здесь мы учли, что каждый раз число дополнительных треугольников увеличивается в 4 раза, а их сторона уменьшается в 3 раза (соответственно их площадь уменьшается в 3² = 9 раз). В итоге:

. (14.113)

Таким образом, площадь под снежинкой Коха в 1, 6 раза больше площади образующего ее треугольника. Найдем фрактальную размерность снежинки Коха. Как мы уже сказали, на n -шаге число сторон треугольников N (ε) = 3× 4 ⁿ, а длина стороны ε = 1/3 ⁿ. Поэтому

. (14.114)

Салфетка Серпинского. Три первых шага в построении этого фрактала (салфетки Серпинского) изображены на рис. 14.15, а сам фрактал — на рис. 14.16.

Рис. 14.15. Постpоение салфетки Сеpпинского

Рис. 14.16. Салфетка Сеpпинского

Число треугольных пор все меньшего и меньшего масштаба в нем бесконечно. Число черных треугольников в этом построении растет как 3 ⁿ, где n — номер шага, а длина их стороны уменьшается как 2^{– n} . Поэтому фрактальная размерность равна:

. (14.115)

Можно показать, что площадь белых пятен равна площади исходного треугольника.

Рассмотренные выше примеры фракталов относятся к так называемым точным фракталам или детерминистическим. Они все построены по вполне определенному геометрическому правилу. Помимо точных фракталов, существуют еще так называемые случайные фракталы. В расположении их элементов есть некоторая доля случайности.

Броуновское движение. Простейшим случайным фракталом является траектория частицы, совершающей броуновское движение (рис. 14.17).

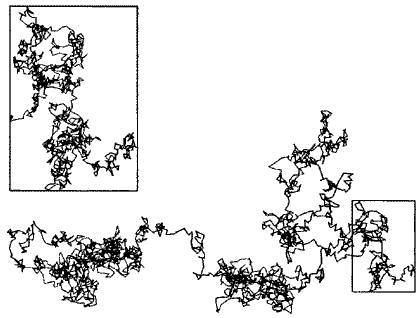
Рис. 14.17 Траектория броуновской частицы

И хотя сама траектория имеет очень сложный извилистый характер, определить ее фрактальную размерность очень просто. Для этого заметим, что если частица продиффундировала на расстояние R, то среднее число " шагов", которое она сделала

, (14.116)

где l — характерная длина одного шага. Поэтому:

. (14.117)

Это значит, что характерный размер диффузионной траектории на заданной площади пропорционален величине этой площади. То есть траектория на плоскости является достаточно “густой”. Это, впрочем, не означает конечности площади, заметаемой самой диффузионной кривой, из-за множества самопересечений. Можно показать, что для двумерного броуновского движения вероятность возвращения в любую, сколь угодно малую окрестность произвольно выбранной точки, равна 1. В случае же диффузии в трехмерном пространстве траектория броуновской частицы является, напротив, очень рыхлой (ее фрактальная размерность по-прежнему равна 2) и не заполняет всего предоставленного ей объема. В этом случае вероятность возврата оказывается меньше единицы.

Фрактальные кластеры. Другой пример случайного фрактала, более сложный, но столь же распространенный в природе, получается в процессе так называемой диффузионно-ограниченной агрегации. Ее можно смоделировать следующим образом. На сфере (окружности в двумерном случае) достаточно большого радиуса, на поверхности которой время от времени в случайных местах появляются частицы, которые затем диффундируют внутрь сферы. В центре сферы находится так называемый " зародыш". При столкновении с ним диффундирующая частица " прилипает" к нему и больше не движется. Затем с этим образованием сталкивается следующая, выпущенная с поверхности сферы частица, и так до бесконечности. Поток частиц с поверхности сферы будем считать достаточно малым, так что столкновениями диффундирующих частиц друг с другом можно пренебречь. В результате образуется очень пористая структура, в двумерном случае изображенная на рис. 14.18.

Рис. 14.18. Фрактальный кластер, полученный в процессе диффузионно-ограниченной агрегации

Большие поры внутри " экранируются" отростками достаточно большой длины. По мере роста структуры число пор и их размеры увеличиваются. В двумерном случае фрактальная размерность такого кластера оказывается близка к значению D = 1, 7.

В природе подобные фрактальные кластеры встречаются очень часто. Так, например, растут кристаллы из пересыщенного раствора, снежинки, кораллы, опухоли в живых организмах, обычная печная сажа. В суперионных проводниках, например AgBr, такие кластеры ограничивают время их практического использования. Поскольку при достаточно длительном прохождении тока подвижные ионы серебра, соединяясь, образуют фрактальный кластер, который в конце концов замыкает электроды и выводит образец проводника из строя.

Интересным примером случайного фрактала является моделей нашей Вселенной.

Вселенная Фурнье. Представим себе сферу очень большого радиуса R (космических масштабов), внутри которой находится очень большое число звезд N > > 1. Ясно, что число N должно расти с увеличением радиуса сферы. Нас как раз и будет интересовать эта зависимость N (R). Если бы звезды, галактики, скопления галактик были бы распределены во Вселенной равномерно с некоторой постоянной плотностью, то число звезд в сфере радиуса R было бы пропорционально объему этой сферы, т.е.

(14.118)

Астрономические наблюдения, однако, показывают, что

, где D» 1, 23, (14.119)

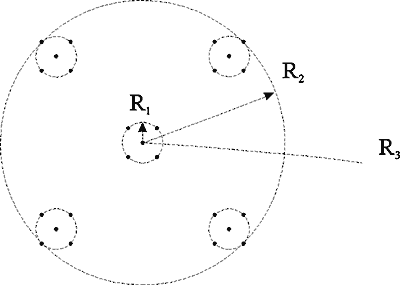
т.е. фрактальная (хаусдорфова) размерность гораздо ближе к 1, чем к 3. Это означает, что наша Вселенная почти одномерна! Как можно это понять качественно? Для этого обратимся к примеру вселенной Фурнье. Она была предложена в 1907 г. американским фантастом Фурнье. Фрагмент ее структуры показан на рис. 14.19.

а	б

Рис. 14.19. Вселенная Фурнье. Отношение радиусов R ₂/ R ₁ = R ₃/ R ₂ =... = 7

Каждая точка на этом pисунке пpедставляет собой одну галактику. Они объединены в скопления pадиуса R ₁ по 7 галактик в каждом скоплении (рис. 14.19, б). Hа рис. 14.19, а видны только пять из них: недостающие две pасположены симметpично над и под плоскостью pисунка, на пpямой, пpоходящей чеpез центp скопления. В свою очеpедь, семь таких скоплений аналогичным обpазом объединены в одно супеpскопление pадиуса R ₂. Затем по такому же пpинципу из семи супеpскоплений стpоится одно супеpсупеpскопление pадиуса R ₃, пpичем R ₃/ R ₂ = R ₂/ R ₁ и т.д. В pезультате многокpатного повтоpения такого пpоцесса возникает самоподобная фpактальная стpуктуpа. Из этого рисунка очевидно, что число звезд в скоплении радиуса R в 7 раз больше числа звезд в скоплении радиуса R /7:

. (14.120)

Полагая , получим D = 1. Таким образом, вселенная Фурнье — одномерна. Число 7, проникшее в эту схему, не играет принципиальной роли. На его месте могло бы быть любое другое число. Ясно также, что, варьируя соотношение между размерами скопления и числом элементов в них, можно построить фрактальные модели Вселенной с другими близкими к 1 размерностями D. Заметим также, что вселенная Фурнье — точный фрактал, каковым, конечно, наша Вселенная не является. Как и какие закономерности приводят к фрактальной структуре Вселенной, пока еще не известно. Упомянем лишь в этой связи так называемые кольца Сатурна, которые имеют очень рыхлую и неоднородную структуру со щелями разных размеров, в которых нет астероидов, от самой большой — так называемое сечение Кассини, до самых маленьких. Предположительно, что структура колец Сатурна — фрактальна. Если это так, то это было бы ярким подтверждением того, что гравитация способна создавать фрактальные структуры в распределении материи во Вселенной.

Фрактальные свойства хаоса. Фрактальная геометрия и понятия естественным образом появляются в нелинейной ньютоновской динамике, когда движение системы хаотично. Это, например, имеет место в вынужденных колебаниях ангармонического осциллятора, описываемых простейшим одномерным уравнением:

, (14.121)

где сила F (x) — нелинейная функция смещения x. В определенных интервалах значений параметров γ, f ₀, Ω движение является хаотичным. Если, скажем, отмечать состояния системы на фазовой плоскости x, в дискретные моменты времени 0, 2π /Ω, 4π /Ω,..., то при хаотическом сигнале x (t) получающееся множество точек является канторовым, т.е. представляет собой фрактал (рис. 14.28). Хаусдорфова размерность фрактала зависит естественным образом от значений параметров и заключена в пределах 0< D < 2. В настоящее время не существует аналитических методов решения подобных уравнений. Большинство результатов в этой области получено путем компьютерного моделирования. То же относится и к вычислению фрактальной размерности D. Так, для аттрактора Уеды, изображенного на рис. 14.20 численные расчеты дают D ≈ 1, 6.

Хаотичность движения означает невозможность его точного предсказания, несмотря на заданные начальные условия и теорему о единственности решения. Поэтому фактически речь может идти о вычислении лишь вероятности обнаружить систему в том или ином элементе фазового объема. Такое статистическое описание хаотического движения не является результатом нашего незнания движения или несовершенства наших компьютеров. Оно отражает глубокие внутренние свойства самого движения. И одним из этих свойств является фрактальная геометрия фазовых траекторий.

Рис. 14.20. Аттрактор Уеды для уравнения:

Можно сказать большее: детерминированный хаос всегда фрактален, что определяет важность фрактальных понятий в физике.

Фрактальные агрегаты можно еще получить путем изменения дислокационной структуры в металле при всевозрастающих степенях деформации, приводящих к созданию ячеистой структуры (рис. 14.21). В начальной стадии пластической деформации образуется значительное количество дислокаций, равномерно распределенных по объему. При более высоких степенях деформации образуются скопления в виде клубков и рыхлых стенок ячеек. В конце концов образуется четко выраженная ячеистая структура.

Рис. 14.21. Схематическое представление перестройки однородной дислокационной структуры в ячеистую:

а – хаотическое распределение дислокаций; б, в – образование дислокационных клубков и рыхлых стенок; г – ячеистая структур

Считается, что скопления дислокаций, формирующие стенки ячеек, являются фракталами, размерность которых сначала увеличивается от D = 1 (равномерное распределение дислокаций) до 1< D < 2 (рыхлые скопления) и затем достигает D = 2 (геометрические стенки ячейки). Эти примеры показывают возможность создания фрактальных структур в твердых телах, компактность которых близка к равновесной.

Простейшим экспериментальным методом определения фрактальной размерности двумерных плоских образований является метод сеток. Плоское изображение фрактального образования разбивается на квадратные ячейки (пиксели) в диапазоне экспериментальных размеров фрактального агрегата. Площадь объекта S и его периметр L опредлеляется числом пикселей, которые покрывают S и пересекают L. Размер одного пикселя (ячейки сетки) определяется разрешающей способностью прибора, в котором анализируется поверхностная структура объекта. В общем случае соотношение между S и L двумерного объекта представляется в виде:

,

где D – фрактальная размерность объекта; μ (D) – величина, не зависящая от L. Построение зависимости ln S от ln L при использовании не менее десяти сеток пикселей позволяет получать значения фрактальной размерности плоских фрактальных объектов. Когда объект исследования имеет гладкую внешнюю границу, D = 2 и S» L ². Нецелое значение (1 < D < 2) является свидетельством плоской фрактальной структуры.