Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Ергодичні випадкові процеси.

Поряд з розглянутим способом осереднення реалізацій випадкового процесу 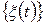за ансамблем у фіксовані моменти часу 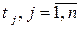, існує спосіб опису властивостей випадкового процесу шляхом осереднення за часом окремих вибіркових функцій ансамблю. Наприклад, для 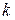- ої вибіркової функції випадкового процесу 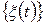, що зображено на рис. 3.3, середнє значення і автокореляційна функція 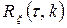визначаються наступними виразами

(3.4)

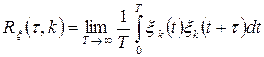(3.5)

Якщо випадковий процес 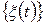стаціонарний і параметри та 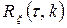, що визначені співвідношеннями (3.4) і (3.5) однакові для різних вибіркових реалізацій, то випадковий процес 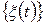називається ергодичним. Для ергодичного випадкового процесу середнє значення і автокореляційна функція (а також і інші моменти, що одержані осередненням за часом) рівні відповідним середнім за ансамблем 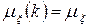та . Слід зазначити, що тільки стаціонарні процеси можуть володіти властивостями ергодичності.

Ергодичні випадкові процеси складають дуже важливий клас випадкових процесів. На практиці виконання умови ергодичності надає можливість уникнути повторення великої кількості експериментів для визначення статистичних характеристик досліджуваного випадкового процесу 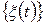, оскільки для цього вистачить виміру однієї єдиної вибіркової реалізації.