
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделі стаціонарних процесів з неперервним часом.
|
|
Моделі фізичних процесів з неперервним і дискретним часом. Статистичне оцінювання
Моделі стаціонарних процесів з неперервним часом. Моделі фізичних процесів із дискретним часом. Статистичне оцінювання характеристик випадкових процесів. Часовий ряд
Моделі стаціонарних процесів з неперервним часом.
Основні пояснення, узагальнені означення стосовно моделей стаціонарних випадкових процесів було зроблено у підрозділі 3.4 (лекція 3). У цьому підрозділі докладно зупинимось на розгляді більш строгих у математичному плані означень, що стосуються стаціонарних випадкових процесів з неперервним часом. Наведені далі означення стосуються безпосередньо стаціонарних випадкових процесі з кінцевою потужністю, які застосовуються у системах, що реалізуються фізично. Такі процеси описуються математичними моделями гільбертових випадкових процесів. Розглянемо докладніше основні означення, що стосуються вказаних процесів
ОЗНАЧЕННЯ 4.1. Гільбертів процес  ,
, 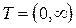 або
або 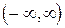 , називається слабо стаціонарним (стаціонарним у широкому розумінні або стаціонарним за О.Я.Хінчиним, іноді стаціонарним другого порядку), якщо його перші два моменти не залежать від початку відліку процесу, тобто коли
, називається слабо стаціонарним (стаціонарним у широкому розумінні або стаціонарним за О.Я.Хінчиним, іноді стаціонарним другого порядку), якщо його перші два моменти не залежать від початку відліку процесу, тобто коли

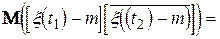
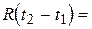
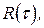
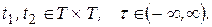 (4.1)
(4.1)
Для такого процесу кореляційна функція  залежить лише від різниці
залежить лише від різниці  двох моментів часу.
двох моментів часу.
ОЗНАЧЕННЯ 4.2. Процес  називається стаціонарним (у вузькому сенсі), коли послідовність його скінченновимірних функцій розподілу не залежить від початку відліку процесу в часі, тобто коли при довільних
називається стаціонарним (у вузькому сенсі), коли послідовність його скінченновимірних функцій розподілу не залежить від початку відліку процесу в часі, тобто коли при довільних 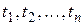 таких, що
таких, що 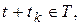
 незалежно від
незалежно від  маємо
маємо

 . (4.2)
. (4.2)
Для стаціонарних у вузькому сенсі процесів математичне сподівання є постійною величиною, а кореляційна (автокореляційна) функція залежить лише від різниці аргументів, тобто процес, стаціонарний у вузькому розумінні, завжди є також слабо стаціонарним, коли він гільбертів. Обернене твердження, взагалі кажучи, невірне. Виняток становлять дійсні гауссівські гільбертові процеси. (Для комплексних гауссівських процесів обернене твердження також не має місця).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
ОЗНАЧЕННЯ 4.3. Слабо стаціонарні випадкові процеси  і
і 
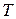 - піввісь або вся вісь, називають стаціонарно зв'язаними, коли їх взаємна коваріаційна функція
- піввісь або вся вісь, називають стаціонарно зв'язаними, коли їх взаємна коваріаційна функція
 ,
,
тобто залежить лише від різниці аргументів 
Із цього означення випливає, що і для стаціонарно зв'язаних процесів кореляційна функція
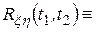

також залежить тільки від різниці двох моментів часу 
Випадковий вектор 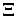 називається слабо стаціонарним, коли всі його компоненти стаціонарно зв'язані (а значить і слабо стаціонарні).
називається слабо стаціонарним, коли всі його компоненти стаціонарно зв'язані (а значить і слабо стаціонарні).
Позначимо через  нормовану кореляційну функцію стаціонарного процесу, тобто
нормовану кореляційну функцію стаціонарного процесу, тобто
 .
.
Оскільки  то
то 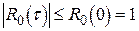 .
.
Має місце наступна теорема.
ТЕОРЕМАХІНЧИНА. Для того, щоб функція  , являла собою нормовану кореляційну функцію деякого дійсного слабо стаціонарного гільбертового випадкового процесу
, являла собою нормовану кореляційну функцію деякого дійсного слабо стаціонарного гільбертового випадкового процесу 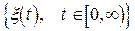 , що задовольняє умові
, що задовольняє умові
 ,
,
необхідно і достатньо, щоб її можна було подати у вигляді
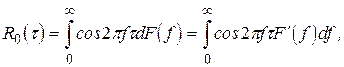 (4.3)
(4.3)
де  - деяка функція розподілу
- деяка функція розподілу 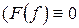 при
при 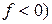 , яку називають спектральною функцією.
, яку називають спектральною функцією.
Останнє означає, що  задовольняє всім властивостям функції розподілу, визначеним згідно з (3.22)(лекція 3), а
задовольняє всім властивостям функції розподілу, визначеним згідно з (3.22)(лекція 3), а  при цьому можна розглядати як характеристичну функцію для
при цьому можна розглядати як характеристичну функцію для  .
.
А.Я.Хінчин опублікував своє доведення цієї теореми в 1934 році в роботі " Korrelation Theorie der stationaren stochastischen Prozesse", Math. Ann. Bd. 190. H. J. p.p 604-615.
Функція  - дійсна, невід'ємна, обмежена
- дійсна, невід'ємна, обмежена  , неперервна “зліва”, її числові значення являють собою ту частину середньої потужності флуктуацій процесу
, неперервна “зліва”, її числові значення являють собою ту частину середньої потужності флуктуацій процесу  , яка припадає на частоти, що не перевищують фіксованої частоти
, яка припадає на частоти, що не перевищують фіксованої частоти 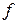 .
.
Функція  може бути розкладена на дві адитивні компоненти (в загальному випадку - на три):
може бути розкладена на дві адитивні компоненти (в загальному випадку - на три):
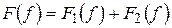 ,
,
де  - кусково-постійна, так звана функція стрибків, яка характеризує собою дискретний спектр процесу
- кусково-постійна, так звана функція стрибків, яка характеризує собою дискретний спектр процесу  (його майже періодична складова),
(його майже періодична складова), 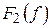 неперервна (точніше, абсолютно неперервна) функція, яка характеризує собою неперервний спектр процесу
неперервна (точніше, абсолютно неперервна) функція, яка характеризує собою неперервний спектр процесу  (див. рис. 4.1).
(див. рис. 4.1).



Рис. 4.1
Відповідно до цього і  може бути розкладена на дві адитивні компоненти. Процес
може бути розкладена на дві адитивні компоненти. Процес  також можна представити у вигляді відповідних двох компонент, одна з яких має чисто розривну, кусково-постійну спектральну функцію (майже періодична компонента), а друга - неперервну спектральну функцію. Ці дві компоненти не обов'язково одночасно існують.
також можна представити у вигляді відповідних двох компонент, одна з яких має чисто розривну, кусково-постійну спектральну функцію (майже періодична компонента), а друга - неперервну спектральну функцію. Ці дві компоненти не обов'язково одночасно існують.
Якщо 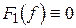 , тобто коли спектральна функція
, тобто коли спектральна функція 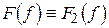 і є диференційованою, то її похідна
і є диференційованою, то її похідна  називається спектральною щільністю потужності (більш точно, коли
називається спектральною щільністю потужності (більш точно, коли  абсолютно неперервна, тоді
абсолютно неперервна, тоді  . У цьому випадку спектральна щільність потужності визначається як косинус-перетворення Фур'є від кореляційної функції:
. У цьому випадку спектральна щільність потужності визначається як косинус-перетворення Фур'є від кореляційної функції:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
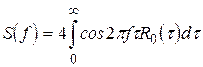 . (4.4)
. (4.4)
Розмірність  - потужність на Гц.
- потужність на Гц.
Критерієм, що забезпечує коректність застосування (тобто існування спектральної щільності) останньої формули (4.4), може бути існування інтегралу 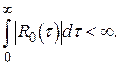
За допомогою спектральної функції  або спектральної щільності потужності
або спектральної щільності потужності  визначається середня потужність флуктуацій стаціонарного випадкового процесу в діапазоні частот
визначається середня потужність флуктуацій стаціонарного випадкового процесу в діапазоні частот  у відповідності з формулою (див. рис. 4.2)
у відповідності з формулою (див. рис. 4.2)
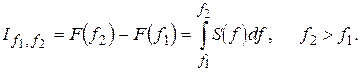
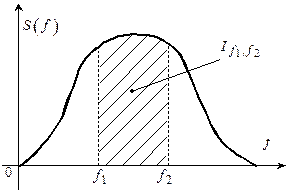
Рис. 4.2
Остання формула має місце, якщо існує  . В загальному випадку по заданій нормованій кореляційній функції
. В загальному випадку по заданій нормованій кореляційній функції  спектральна функція знаходиться оберненим перетворенням Фур'є-Стілтьєса
спектральна функція знаходиться оберненим перетворенням Фур'є-Стілтьєса
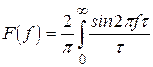
 (4.5)
(4.5)
де 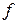 - точка неперервності
- точка неперервності  .
.
Таким чином, теорема Хінчина дозволяє встановити частотні властивості флуктуацій стаціонарних фізичних процесів з неперервним часом, якщо відома їх кореляційна функція.
ПРИКЛАД 4.1. Дуже часто в практичних застосуваннях зустрічаються моделі сигналів з так званою експоненційно-косинусною кореляційною функцією, що задається виразом
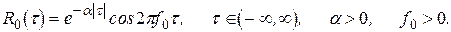
(В загальному випадку 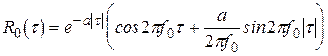 ). Це так звані вузькосмугові випадкові процеси.
). Це так звані вузькосмугові випадкові процеси.
На рис. 4.3 наведені графіки кореляційних функцій
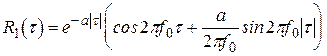 ,
,  ,
,  ,
,
 .
.
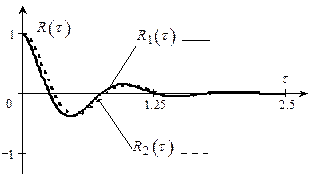
Рис. 4.3
Подібну кореляційну функцію мають процеси на виході акустичного резонатора в коливному режимі, або відгук коливного електричного  контура високої добротності, коли на нього діє ’’білий шум’’. Тут
контура високої добротності, коли на нього діє ’’білий шум’’. Тут 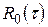 - в одиницях потужності,
- в одиницях потужності, 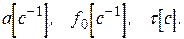
В цьому випадку 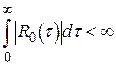 , а значить існує спектральна щільність
, а значить існує спектральна щільність  , яка визначається формулою (4.4), а саме
, яка визначається формулою (4.4), а саме
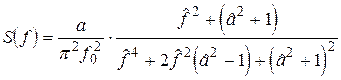 ,
,
де введенні позначення
 і
і 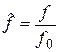 .
.
Наведена функція  має точки екстремуму
має точки екстремуму
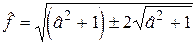 .
.
З цього виразу видно, що при 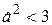 точка екстремуму дійсна, в цьому випадку
точка екстремуму дійсна, в цьому випадку  має єдиний максимум, який із зменшенням
має єдиний максимум, який із зменшенням  від
від 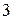 до
до  переміщується від
переміщується від  до
до 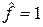 і збільшується за абсолютним значенням, вироджуючись при
і збільшується за абсолютним значенням, вироджуючись при 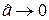 в
в  - функцію (див. рис. 4.4). При
- функцію (див. рис. 4.4). При  максимум
максимум  відсутній.
відсутній.

Рис. 4.4
У наведеному прикладі спектральна функція
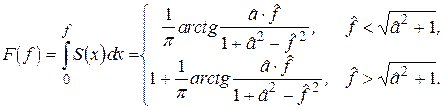
В діапазоні  лежить половина потужності цього процесу.
лежить половина потужності цього процесу.
Якщо в даному прикладі взяти 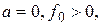 то тоді функція
то тоді функція  буде не інтегрованою по модулю і для визначення спектральної функції потрібно користуватися загальною формулою (4.5). У цьому випадку
буде не інтегрованою по модулю і для визначення спектральної функції потрібно користуватися загальною формулою (4.5). У цьому випадку
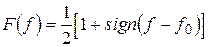 .
.
Отже, маємо

На рис. 4.5 показаний графік спектральної функції для цього випадку.
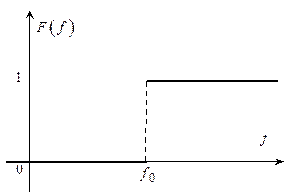
Рис. 4.5
Таким чином, при 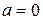 маємо
маємо
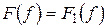 і
і  ,
,
тобто одержуємо чисто дискретний спектр.
|
|
