
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математичних моделей фізичних процесів та об'єктів.
|
|
Як показав огляд робіт вітчизняних і зарубіжних авторів, наведений у [4], на даний час при дослідженні різних фізичних процесів, які супроводжують роботу технічних об'єктів, використовуються інформаційно-вимірювальні системи (ІВС) та прилади, що базуються на застосуванні як детермінованих, так і статистичних методів.
При використанні детермінованих методів в якості вихідної математичної моделі інформаційних сигналів, що надходять від датчиків, встановлених на досліджуваному вузлі, вибирають детерміновану функцію часу. У цьому випадку в якості інформативних найчастіше виступають амплітудно-частотні або фазово-частотні параметри сигналів, що характеризують роботу досліджуваних вузлів різного обладнання.
Наприклад, при вирішенні завдання діагностики, використання детермінованих методів, в основному, зводиться до теоретичного визначення можливих діагностичних ознак і порівнянню їх з результатами аналізу експериментальних даних. Якщо останні істотно відрізняються від результатів, отриманих теоретично, то робиться висновок про наявність дефекту в досліджуваному вузлі. За своєю суттю ці методи застосовні в тому випадку, коли однотипні результати всіх спостережень при реалізації одних і тих же початкових умов абсолютно ідентичні, а також якщо вимірюється один і той же параметр (ознака) в одних і тих же умовах. Така ситуація або сильно ідеалізована, або спостерігається при дуже низькій точності використовуваних вимірювальних приладів, коли випадкові впливу на виміри не сприймаються вимірювальними приладами. Отже, при детермінованому підході відпадає необхідність у багаторазових вимірах, тому що вони всі однакові і висновок про технічний стан вузла може бути зроблений по одному виміру. Проте завжди є можливість, підвищуючи точність кожного окремого вимірювання, виявити неповторність результатів вимірювання в описаній вище ситуації. Тоді виникає питання, що з отриманого ряду чисел вважати результатом проведеного виміру. Тому застосування детермінованих методів не можна вважати задовільним і аргументованим, оскільки переважна більшість вимірюваних процесів, що виникають у досліджуваних вузлах різного устаткування, носять випадковий характер за своєю природою, тобто їх реалізації змінюються від спостереження до спостереження. Таким чином, виключена можливість одержання по одному спостереженню практично достовірної відповіді про технічний стан вузлів, що діагностуються.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Невипадкові або детерміновані сигнали зручно розглядати як окремий (вироджений) випадок випадкових процесів за умови, що дисперсія таких процесів прямує до нуля. Такий спосіб суджень дуже часто зустрічається як в теоретичних, так і в прикладних наукових роботах.
Моделі невипадкових сигналів, як правило, простіше, ніж моделі випадкових перешкод і найчастіше являють собою суму або твір елементарних (в більшості випадків гармонійних) простих функцій, тому детально їх розглядати не будемо, вони вже розглядалися в курсі основ теорії кіл, процесів та сигналів в радіотехніці. Наведемо лише деякі приклади:
1)  - просте гармонійне коливання, задане на одному з континуальних інтервалів часу
- просте гармонійне коливання, задане на одному з континуальних інтервалів часу 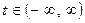 або
або  або
або  . Тут
. Тут  - позитивний числовий параметр, іменований амплітудою, -
- позитивний числовий параметр, іменований амплітудою, -  числовий параметр, іменований початковою фазою, і
числовий параметр, іменований початковою фазою, і 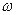 - кутова частота
- кутова частота  ,
,
2)  - амплітудно-модульоване коливання,
- амплітудно-модульоване коливання, 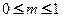 ,
, 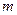 - глибина модуляції,
- глибина модуляції, 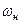 - несуча частота,
- несуча частота,  , зокрема
, зокрема  , де
, де 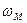 частота модуляції, звичайно
частота модуляції, звичайно  ;
;
3)  - затухаючий ритмічний процес, (не періодичний).
- затухаючий ритмічний процес, (не періодичний).
У випадку дослідження фізичних процесів за допомогою ІВС, заснованих на статистичних методах, створюється можливість по серії результатів певного вимірювального експерименту рекомендувати алгоритм, за яким обчислюється найкраще в імовірнісному сенсі наближення вимірюваного параметра. Крім того, при використанні ІВС, що базуються на статистичних методах, враховується міра неправильних рішень про технічний стан діагностуються вузлів, а також можна оцінити середню кількість можливих невірних висновків, їх розкид і ін. Основними параметрами, які використовуються в якості діагностичних ознак при застосуванні ІІC, що базуються на статистичних методах, є математичне сподівання, дисперсія досліджуваних реалізації сигналів, а з функціональних характеристик - кореляційна функція, енергетичний спектр і одномірна функція розподілу.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Невід'ємною частиною ІВС технічної діагностики є безпосередньо сам об'єкт діагностики. Для впевненого проведення діагностики того або іншого вузла досліднику, з одного боку, необхідно мати математичну модель, яка на підставі фізики явищ досить достовірно описувала б вимірювані процеси, що у досліджуваних вузлах, а з іншого боку, потрібно мати ІВС, побудованої з урахуванням апріорних даних про інформаційні сигнали, які можуть бути отримані за результатами аналізу математичної моделі досліджуваних процесів. При цьому в хронологічному плані модель є первинною, а методи (детерміновані або статистичні), покладені в основу використовуваної ІВС, - вторинними, оскільки вони розробляються відповідно до обраної моделі.
Аналіз робіт вітчизняних і зарубіжних авторів [3, 4] показав, що використання статистичних методів обробки інформаційних сигналів є більш обґрунтованим в порівнянні з детермінованими методами, оскільки багато фізичних процесів, що супроводжують роботу досліджуваних вузлів електротехнічного обладнання, носять випадковий характер за своєю природою. На підставі проведеного аналізу цілого ряду наукових робіт[3, 4], можна стверджувати, що при створенні ІВС діагностики промислового обладнання необхідно використовувати статистичні методи обробки інформаційних сигналів, тобто в основу такої ІВС має бути покладена імовірнісна математична модель.
Моделі випадкових сигналів. Торкаючись питань побудови моделей випадкових процесів, коротко зупинимося на наступному прикладі. Розглянемо питання побудови математичної моделі деякого технічного об'єкта для вирішення завдання діагностики. Математична модель об'єкта діагностики задається багатовимірним вектором
 , (2.5)
, (2.5)
де 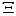 -
-  - мірний вектор, компонентами якого є
- мірний вектор, компонентами якого є  - вихідних функцій
- вихідних функцій 
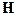 -
- 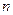 - мірний вектор, компонентами якого є
- мірний вектор, компонентами якого є 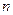 вхідних функцій
вхідних функцій 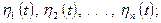
 -
- 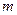 - мірний вектор, компонентами якого є
- мірний вектор, компонентами якого є 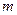 внутрішніх функцій об'єкта діагностики
внутрішніх функцій об'єкта діагностики 
 - поточний час, а
- поточний час, а 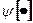 - деякий в загальному випадку нелінійний функціонал від перелічених вище векторів, залежний від часу
- деякий в загальному випадку нелінійний функціонал від перелічених вище векторів, залежний від часу  .
.
Коротко зупинимося на описі компонент векторів, і Ф, що входять в модель (2.5). При стохастичному підході до побудови моделі (2.5) математична модель впливу задається багатовимірним вектором Н, компоненти якого можуть бути задані різними класами випадкових процесів. При цьому необхідно враховувати фізичний характер реальних впливів. Для побудови математичних моделей впливів, які представляють собою деякий імпульсний потік, можна скористатися класом випадкових процесів, що володіють безмежно подільними законами розподілу [3]. Цей клас процесів найбільш адекватно описує імпульсні процеси в електротехнічному обладнанні, що викликають вібрації окремих його вузлів, або процеси акустичної емісії, що виникають в твердому тілі при його навантаженні, або, наприклад, процеси виникнення електричних розрядів в ізоляції при подачі високої напруги.
Вибір даного класу процесів при побудові моделей є принциповим, оскільки для нього відомий загальний вид канонічного представлення характеристичної функції, яка повністю задає цей процес. Опис деяких властивостей даного класу процесів, а також фізичне обґрунтування їх застосування наведено в [3, 4].
Об'єкт діагностики характеризується - мірним вектором Ф, до якості компонент якого зазвичай вибираються числові невипадкові функції Ці функції можуть володіти різними властивостями, притаманними досліджуваним об'єктам, а саме, можуть бути лінійними, нелінійними, інваріантними за часом і т.д.
Внутрішньо стан діагностується характеризується числовими параметрами, що входять у функції
Поява тих або інших дефектів в діагностується викликає зміна його внутрішнього стану, тобто зміна параметрів, що входять у функції Це, в свою чергу, призводить до зміни характеру відгуку діагностується, який описується - мірним вектором з компонентами
на вплив, що характеризується раніше розглянутим вектором Н. Тобто, вимірюючи і аналізуючи компоненти вектора, можна проводити діагностику досліджуваного об'єкта.
Теоретичне дослідження моделі (2.5) дозволяє обґрунтувати деякі діагностичні ознаки технічного стану діагностується обладнання. Під діагностичними ознаками маються на увазі такі параметри характеризують модель (2.5), які дозволяють із заданою вірогідністю діагностувати технічний стан досліджуваного об'єкта. Ці діагностичні параметри можуть бути укладені у векторах Ф або Н, а вимірюються опосередковано через вектор, пов'язаний з ними виразом (2.5). Фактично діагностика зводиться до вимірювання параметрів, що характеризують вектора Ф і Н через вектор, з подальшим прийняттям рішення за даними попереднього навчання і побудованим вирішальним правилами.
Крім теоретичного обґрунтування діагностичних ознак на підставі аналізу моделі (2.5) виникає питання, які з компонент, що входять в (2.5), вимірювати. Так, досить складно виміряти компоненти породжує процесу, який характеризується вектором Н. Так само складно зробити виміри параметрів, що характеризують внутрішній стан системи і вхідних в вектор Ф. Найдоступнішими в сенсі проведення діагностичних вимірів виявляються компоненти вектора 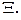
Таким чином, системи статистичної діагностики орієнтуються, в основному, на вимірювання компонент вектора Визначальним моментом при побудові моделі (2.5) є вибір класу процесів, що характеризують вектор впливів Н, а також визначення власної функції Ф, що характеризує діагностується об'єкт. У цьому випадку виходять із деяких передумов, що характеризують фізичний процес, який супроводжує роботу конкретного досліджуваного вузла. Багато моделей таких процесів ґрунтуються на тому, що в точці виміру в будь-який фіксований момент часу досліджуваний процес можна розглядати як алгебраїчну суму великого числа випадкових величин, що характеризують енергію, що приходить від різних випадкових джерел, розташованих в просторі на деякій відстані від цієї точки. Такі моделі можна використовувати при описі шумових і вібраційних процесів і полів акустичної емісії, що виникають в твердому тілі при його механічному навантаженні або, наприклад, процесів виникнення електричних розрядів в ізоляції при подачі високої напруги.
У найпростішому одновимірному випадку задача побудови математичної моделі досліджуваного фізичного процесу може бути зведена до класичної задачі аналізу відгуку системи з імпульсною перехідною функцією при впливі на її входи деякого процесу, який в теорії систем зазвичай називають породжуючим. Зазвичай при вирішенні подібних задач вважають, що для такого породжуючого процесу відомі деякі його характеристики. Схематично цю задачу можна представити таким чином
 |




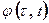
 |
Рис. 2.1
Інакше це може бути записано у вигляді стохастичного інтегрального представлення такого виду
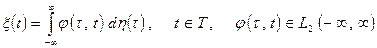 , (2.6)
, (2.6)
при кожному фіксованому  . Таким чином, на рис.2.1 зображена одномірна математична модель вимірюваного при діагностики деякого вузла процесу, яка записана у вигляді стохастичного інтегрального представлення.
. Таким чином, на рис.2.1 зображена одномірна математична модель вимірюваного при діагностики деякого вузла процесу, яка записана у вигляді стохастичного інтегрального представлення.
У цьому представленні, як говорилося вище,  - породжуючий процес, в якості якого зазвичай вибирається процес, для якого відомі повні імовірнісні характеристики, а саме, функція розподілу
- породжуючий процес, в якості якого зазвичай вибирається процес, для якого відомі повні імовірнісні характеристики, а саме, функція розподілу 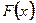 або характеристична функція
або характеристична функція 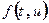 ,
, 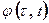 - імпульсна перехідна функція, яка характеризує об'єкт, який діагностується (в математиці у якості такої функції використовується інтегрована по
- імпульсна перехідна функція, яка характеризує об'єкт, який діагностується (в математиці у якості такої функції використовується інтегрована по 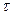 с квадратом числова невипадкова функція, тобто функція, що характеризує систему з кінцевою потужністю, або фізично реалізовану систему). І, нарешті,
с квадратом числова невипадкова функція, тобто функція, що характеризує систему з кінцевою потужністю, або фізично реалізовану систему). І, нарешті, 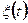 - вимірюваний випадковий процес. Визначення цього процесу нагадаємо у наступній лекції.
- вимірюваний випадковий процес. Визначення цього процесу нагадаємо у наступній лекції.
Контрольні запитання
1. Яка основна особливість функціональних моделей?
2. Дати визначення статичної і динамічної, стаціонарної й нестаціонарної, лінійної та нелінійної математичних моделей?
3. Що розуміють під ієрархією математичних моделей?
4. У чому полягає принцип декомпозиції при математичному моделюванні складного фізичного об'єкта?
5. Що мається на увазі під мірністю математичної моделі?
6. Що розуміють під математичними моделями мікро і макрорівня?
7. Яка найбільш поширена форма подання динамічної моделі мікрорівня?
8. Яка особливість подання математичної моделі мікрорівня в інтегральній формі?
9. Для математичного моделювання яких об'єктів зазвичай застосовують диференційно-функціональні рівняння?
10. Які види рівнянь використовуються як математичних моделей при описі еволюції біологічної популяції?
11. Навести приклади математичних моделей невипадкових сигналів, що характеризують фізичні процеси, супроводжуючих роботу технічних систем?
12. У якій формі найбільш часто задається математична модель, що характеризує випадкові фізичні процеси?
13. Навести приклад випадкової моделі (для одновимірного випадку), фізичного процесу, який супроводжує роботу технічного об'єкта?
|
|
