
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ієрархія математичних моделей і форми їх представлення.
|
|
При математичному моделюванні досить складного технічного об'єкта (ТО) описати його поведінку однієї математичною моделлю (ММ), як правило, не вдається, а якщо така ММ і була б побудована, то вона виявилася б занадто складною для кількісного аналізу. Тому до таких ТО зазвичай застосовують принцип декомпозиції. Він полягає в умовному розбитті ТО на окремі простіші блоки й елементи, що допускають їх незалежне дослідження з наступним урахуванням взаємного впливу блоків і елементів один на одного. У свою чергу, принцип декомпозиції можна застосувати і до кожного виділеного блоку аж до рівня досить простих елементів. У такому випадку виникає ієрархія ММ пов'язаних між собою блоків і елементів.
Ієрархічні рівні виділяють і для окремих типів ММ. Наприклад, серед структурних математичних моделей ТО до більш високого рівня ієрархії відносять топологічні математичні моделі, а до більш низького рівня, що характеризується більшою деталізацією ТО, - геометричні математичні моделі.
Серед функціональних математичних моделей ієрархічні рівні відображають ступінь деталізації опису процесів, що протікають в ТО, його блоках або елементах. З цієї точки зору зазвичай виділяють три основних рівня: мікро-, макро- і метарівень.
Математичні моделі мікрорівня описують процеси в системах з розподіленими параметрами (в континуальних системах), а математичні моделі макрорівня - в системах з зосередженими параметрами (в дискретних системах). У перших з них фазові зміни можуть залежати як від часу, так і від просторових координат, а у других - лише від часу.
Якщо в ММ макрорівня число фазових змінних має порядок 104-105, то кількісний аналіз такої ММ стає громіздким і вимагає значних витрат обчислювальних ресурсів. Крім того, при такому великому числі фазових змінних важко виділити суттєві характеристики ТО і особливості його поведінки. У такому випадку шляхом об'єднання та укрупнення елементів складного ТО прагнуть зменшити число фазових змінних за рахунок виключення з розгляду внутрішніх параметрів елементів, обмежуючись лише описом взаємних зв'язків між укрупненими елементами. Такий підхід характерний для математичних моделей метарівня.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
ММ метарівня зазвичай відносять до вищого рівня ієрархії, ММ макрорівня - до середнього, а ММ мікрорівня - до нижчого.
Найбільш поширеною формою подання динамічної (еволюційної) математичної моделі мікрорівня є формулювання крайової задачі для диференціальних рівнянь математичної фізики [3]. Таке формулювання включає диференціальні рівняння з частинними похідними і крайові умови. У свою чергу, крайові умови містять початкові умови - розподіл шуканих фазових змінних в деякий момент часу, які приймаються за початкові, в просторовій області, конфігурація якої відповідає ТО, що розглядається або його елементу, - і граничні умови на кордонах цієї області. При представленні ММ доцільно використовувати безрозмірні змінні (незалежні і шукані) і коефіцієнти рівнянь, скоротив число параметрів, що характеризують ТО, що розглядається.
ММ мікрорівня називають одномірною, двовимірною або тривимірною, якщо шукані фазові змінні залежать від однієї, двох чи трьох просторових координат відповідно. Два останніх типи ММ об'єднують в багатовимірні математичні моделі мікрорівня. Одновимірна ММ мікрорівня, фазові змінні в якої не залежать від часу, має представлення у вигляді системи ОДУ із заданими граничними умовами (у найпростішому випадку одна фазова змінна такої ММ включає лише одне ОДУ і граничні умови).
Оскільки крайової задачі, яка містить диференціальні рівняння з частинними похідними і крайові умови, можна поставити у відповідність інтегральне формулювання [3], то і ММ мікрорівня також може бути представлена в інтегральній формі. При певних умовах інтегральну форму крайової задачі вдається привести до варіаційного формулювання у вигляді функціоналу [3], який допустимо розглядати на деякій множині функцій, що містить шукану функцію. У цьому випадку говорять про варіаційну форму моделі мікрорівня. Шукана функція обертає в нуль варіацію функціонала, тобто є його стаціонарною точкою.
Побудова функціоналу і відповідної йому варіаційної форми моделі мікрорівня зазвичай ґрунтується на деякому змістовному з фізичної точки зору варіаційному принципі механіки або електродинаміки суцільного середовища (наприклад, на принципі мінімуму потенційної енергії континуальної системи в положенні рівноваги або на принципі мінімуму часу проходження світлового променя між двома точками оптично неоднорідного середовища). У цьому випадку стаціонарна точка функціоналу відповідає його екстремального (зокрема, мінімального) значення на допустимому безлічі функцій. Така форма моделі мікрорівня, звана екстремальної варіаційної, дозволяє, порівнюючи значення функціоналу на будь-яких двох функціях з допустимої множини, оцінювати в інтегральному розумінні близькість цих функцій до шуканої. Ця властивість екстремальної варіаційної форми моделі важливо при якісному аналізі ММ і при порівнянні різних наближених рішень відповідної крайової задачі.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
При виконанні деяких обмежень можна побудувати двоїсту варіаційну форму моделі мікрорівня, яка включає пару функціоналів, що досягають в одній і тій же точці стаціонарності рівних між собою альтернативних екстремальних значень (мінімуму і максимуму) [3]. Така форма ММ дає можливість по різниці значень цих функціоналів, обчислених на деякої функції з допустимої множини, кількісно оцінити похибку, що виникає при виборі цієї функції в якості шуканої.
Основною формою динамічної (еволюційної) ММ макрорівня є ЗДР або їх системи разом із заданими початковими умовами. Незалежним змінним у таких ММ буде час, а шукана - фазові змінні, що характеризують стан ТО (наприклад, переміщення, швидкості і прискорення елементів механічних пристроїв, а також прикладені до цих елементів сили і моменти; тиск і витрата рідини чи газу в трубопроводі; напруги і сили струму в електричних ланцюгах і т.п.). У деяких випадках ММ макрорівня вдається представити у інтегральній формі, використовуючи принцип Гамільтона - Остроградського або екстремальний варіаційний принцип Гамільтона.
Якщо еволюцію ТО визначає його стан не тільки в поточний момент часу, але і в певний попередній момент, то ММ макрорівня включає ЗДР виду
u’(t) = f(t, u(t), u(t- 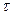 )) (2.3)
)) (2.3)
або
u'{t) = f(t, u(t), u(t- 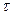 ), u’(t-
), u’(t- 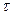 ))
))
щодо шуканої функції u(t). ОДУ типу (2.3) називають рівняннями запізнілого і нейтрального типу відповідно і відносять до диференційно-функціональних [3] рівнянням (ДФР) (або диференціальних рівнянь із відхиляючим аргументом). Найбільш широко ДФР та їх системи представлені в ММ систем автоматичного управління і регулювання. Крім того, ДФР знаходять застосування в моделях біологічних і економічних процесів.
Запізніла реакція ТО на зміну свого стану може визначатися більш ніж одним інтервалом часу t. Тоді ДФР буде включати не одне, а кілька дискретних запізнювань. У більш загальному випадку запізнення може бути безперервним у часі, що призводить, наприклад, для лінійної математичної моделі до інтегро - диференційному рівнянню (ІДР) виду
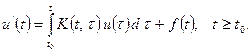 (2.4)
(2.4)
Задану функцію K (t, r) в (2.4) називають ядром цього ІДР, а про ТО, який аналізують кажуть, що він володіє пам'яттю, оскільки його еволюція залежить від всієї передісторії зміни станів ТО.
У статичну математичну модель макрорівня не входить час. Тому вона включає лише кінцеве (у загальному випадку нелінійне) рівняння або систему таких рівнянь (зокрема, систему лінійних алгебраїчних рівнянь - СЛАР). Такий же вигляд мають квазістатична, стаціонарна і квазістаціонарна математичні моделі макрорівня.
Якщо для досліджуваного ТО вдається виділити деякі важливі властивості, що піддаються кількісній характеристиці або сполучення таких властивостей (надійність, довговічність, масу, вартість, будь-якої з визначальних якість ТО вихідних параметрів) і встановити їх зв'язок з фазовими змінними за допомогою дійсної функції, то можна говорити про оптимізацію ТО за критерієм, що виражається цією функцією. Її називають цільовою функцією [3], оскільки її значення характеризує міру (або ступінь) досягнення певної мети вдосконалення ТО відповідно до обраного критерію.
Внаслідок обмеженості наявних ресурсів у реальній ситуації мають сенс лише ті екстремальні значення цільової функції, які досягаються в області можливої зміни фазових змінних ТО, зазвичай обмеженою системою нерівностей. Ці нерівності разом з цільовою функцією і статичною ММ ТО у вигляді кінцевого нелінійного рівняння або систем таких рівнянь входять в математичну формулювання задачі оптимізації ТО за обраним критерієм, званою (у загальному випадку) задачею нелінійного програмування [3]. В окремому випадку лінійної математичної моделі ТО у вигляді СЛАР, лінійних цільової функції і нерівностей говорять про задачу лінійного програмування. До таких задач зазвичай приходять при розгляді проблем техніко-економічного змісту. Задачу оптимізації ТО, яка описується динамічною (еволюційною) ММ макрорівня, відносять до класу задач оптимального керування [3].
Для ММ метауровня характерні ті ж типи рівнянь, що і для ММ макрорівня, але ці рівняння включають фазові змінні, що описують стан укрупнених елементів складних ТО. Якщо визначений закон безперервного переходу ТО з одного стану в інший, то для аналізу ММ метауровня часто використовують апарат передавальних функцій, а при розгляді станів ТО в дискретні моменти часу ЗДР і їх системи переходять в різницеві рівняння відносно значень фазових змінних в ці моменти часу. У випадку дискретної множини станів ТО застосовують також апарат математичної логіки і кінцевих автоматів.
Іноді для складних інформаційних систем вдається перейти до дискретного поданням фазових змінних. Тоді ММ метауровня стає системою логічних співвідношень (СЛС), яка описує процеси перетворення сигналів. Використання СЛС стосовно до таких складних ТО є більш економічним, аніж опис зміни в електричних ланцюгах інформаційної системи напруг і струмів як неперервних функцій часу за допомогою ЗДР або їх систем. До метауровня також відносять імітаційні ММ [3] і ММ масового обслуговувавння [3], що описують функціонування складних обчислювальних та інформаційних систем, виробничих ділянок, ліній, цехів, підприємств та їх об'єднань.
ММ метауровня стосовно еволюції біологічної популяції [3] містить послідовність {хn}, елементи якої характеризували відносну чисельність цієї популяції і задовольняли рекурентному співвідношенню 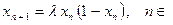 N де
N де 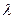 - коефіцієнт розмноження. Це співвідношення можна розглядати як різницеве рівняння по відношенню до ДФУ
- коефіцієнт розмноження. Це співвідношення можна розглядати як різницеве рівняння по відношенню до ДФУ 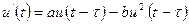 , де u (t) - чисельність популяції в поточний момент часу t,
, де u (t) - чисельність популяції в поточний момент часу t, 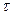 - період біологічного циклу розмноження,
- період біологічного циклу розмноження,  і
і 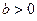 - параметри, що характеризують швидкості відповідно розмноження і вимирання популяції при перенаселенні. Дійсно, наближено замінюючи в ДФУ похідну за часом звичайно-різницевим співвідношенням
- параметри, що характеризують швидкості відповідно розмноження і вимирання популяції при перенаселенні. Дійсно, наближено замінюючи в ДФУ похідну за часом звичайно-різницевим співвідношенням  і позначаючи
і позначаючи  і
і 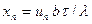 , після перетворень одержимо записане вище різницеве рівняння.
, після перетворень одержимо записане вище різницеве рівняння.
У цьому курсі лекцій обмежимося розглядом ММ макро- і макрорівня.
|
|
