Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Основные свойства сжимающих отображений

Теорема 9.2. Всякое сжимающее отображение метрического пространства Х в себя непрерывно на множестве Х.

3Выберем любую точку х_оÎ Х. Для " e> 0 существует d (e)= > 0 такое, что для " x Î Х ç r_x (x_o, x) < d = из неравенства (9.1) следует, что r_x (f (x_o), f (x)) £ ar_x (x_o, x) < a× = e. Следовательно, отображение непрерывно в точке х_оÎ Х.

Отображение f непрерывное на множестве Х, поскольку оно непрерывное в любой точке х₀ этого множества. 4

Теорема 9.3 (принцип Банаха сжимающих отображений). Всякое сжимающее отображение полного метрического пространства (Х, r) в себя (f: Х Х) имеет неподвижную точку, причем единственную.

Замечание. Х не является пустым множеством.

3Выберем любую точку х ₀ Î Х и построим последовательность (х_n) точек пространства Х по правилу:

x₁ = f (x_o), x₂ = f (x₁), x₃=f (x₂), …, x_n=f (x_{n- 1}). (9.2)

Докажем, что в метрическом пространстве (Х, r) эта последовательность сходится к некоторой точке и что эта точка является неподвижной точкой отображения f.

1. Докажем, что последовательность (x_n) фундаментальная, т.е.

(" e> 0)($N ½ " n, m > N) Þ [ r (x_m, x_n) < e ].

Обозначим r (x₁, x_о) =d (9.3). По условию теоремы f – сжимающее отображение. Используем неравенство (9.1) или определение (9.4). Имеем:

r (f (x ₁), f (x _о)) = r (x ₂, x ₁) £ ar (x ₁, x _о) = a d,

r (f (x ₂), f (x ₁)) =r (x ₃, x ₂) £ ar (x ₂, x ₁) £ a²r (x ₁, x _o) =a²d,

r (f (x ₃), f(x ₂ )) £ ar (x ₃, x ₂) £ a ² r (x ₂, x ₁) = a³d и г.д.

Пользуясь методом математической индукции можно доказать, что r (x_n+1, x_n) £ aⁿd " nÎ N. (9.4)

Выберем произвольные натуральные числа m и n (m> n)и оценим расстояние r (x_m, x_n), воспользовавшись неравенством треугольника и неравенством (9.1).Получим:

r (x_m, x_n) £ r (x_m, x_m-1) + r (x_m-1, x_n) £ r (x_m, x_m-1) + r (x_m-1, x_m-2) +

+ r (x_m-2, x_n) £ r (x_m, x_m-1) + r (x_m-1, x_m-22) + …+ r (x_n+2, x_n+1) + r (x_n+1, x_n) £

£ a^m-1d + a^m-2 d +…+ aⁿd = d (a^m-1 + a^m-2 +…+ aⁿ) = d Þ

Þ r (x_n, x_m) £ d .

Т.к. 0 < a < 1, то a^m < 1. Поэтому r (x_n, x_m) £ d 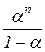(9.5). Предел последовательности 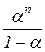равен 0, если n®¥ (т.к. aⁿ – бесконечно убывающая прогрессия). Это значит, что последовательность бесконечно малая, и поэтому

" e> 0 $N (e)½ " n> N Þ 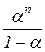< e. (9.6)

Из неравенств (9.5) и (9.6) следует r (x_n, x_m) < e. А это значит, что

" e> 0 $N ½ " n, m > N Þ r (x_m, x_n) < e.

Таким образом, последовательность (9.2) фундаментальная. 4

2. Докажем, что последовательность (9.2) сходится к числу .

По условию теоремы (Х, r) - полное метрическое пространство, (х_n)–фундаментальная последовательность и поэтому она сходится к элементу пространства (Х, r), т.е. существует точка Î Х такая, что

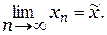
(9.7)

3. Докажем, что - неподвижнаю точка.

Из равенства (9.7) следует, что а из равенства (9.2) f (x_n-1) = x_n. Поэтому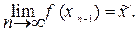

В силу теоремы (9.2) всякое сжимающее отображение является непрерывным. Поэтому 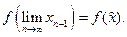Это доказывает неподвижность точки . 4

4. Докажем единственность неподвижной точки.

Используем метод от противного. Предположим, существует еще одна неподвижнаю точка х*. Таким образом существуют две точки , х*Î X такие, что f ()= и f (x*) = x*.

Тогда

r(, x*)=r(f(), f(x*)) £ ar(, x*) Þ r(, x*)£ ar(, x*) Þ r(, x*)(1- a) £ 0. Но это произведение может быть только неотрицательным, поскольку r(, x*) ³ 0 и 0 < a < 1. Таким образом = x*. 4

Замечание. При доказательстве теоремы построен метод нахождения неподвижной точки с помщью последовательности (9.2). Метад нахождения неподвижной точки называется методом итерации, или методом последовательных приближений.

Этим методом можно пользоваться при доказательстве того факта, что уравнение имеет единственное решение как для обычных алгебраических уравнений, так и для дифференциальных уравнений.

Пример. Пусть f –отображение отрезка [ a, b ] в отрезок [ a, b ]. Предполагается также, что функция дифференцируемая, а ее производная удовлетворяет условию:

½ f’ (x)½ £ a (0 < a < 1) " x Î [ a, b ].

Докажем, что уравнение f (x) = x (9.8) имеет единственное решение.

3Заметим, что [ a, b ]– замкнутое множество полного метрического пространства R и поэтому подпространство Х = ([ a, b ], r (x, y) = ½ х-y ½) - полное метрическое пространство (Т.9.1). Данная функция f является отображением этого пространства в себя. Функция f удовлетворяет условиям теоремы Лагранжа на [ a, b ], поэтому:

" x₁, x₂Î [ a, b ] Þ ½ f (x₁) – f (x₂)½ = ½ f’(x) ½ × ½ x₁- x₂ ½ £ a ½ x₁- x₂ ½.

Т.е. заданное отображение f – сжимающее отображение полного метрического пространства в себя. Поэтому по теореме Банаха существует одна точка Î [ a, b ] такая, что f () = . Это точка находится методом итерации с помощью последовательности (9.2). 4