Понятие компактных пространств. Необходимые условия компактности множеств

Определение 8.1. Метрическое пространство X = (X, r) называется компактным или компактом, если из любой последовательности (x_n)элементов этого пространства можно выделить подпоследовательность 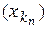, сходящуюся к элементу пространства Х.

Определение 8.2. Множество Е Ì Х называется компактным в метрическом пространства Х, если из любой последовательности элементов множества Е можно выделить подпоследовательность, сходящуюся по метрике r к элементу множества Е, или другими словами: если подпространство (Е, r) - метрическое пространство (X, r)является компактом.

Пример 8.1. Пространство R не является компактом, поскольку существует последовательность (n), nÎ N, из которой нельзя выделить подпоследовательность, которая сходится в R.

Пример 8.2. Всякое конечное множество Е точек метрического пространства (X, r) компактное в этом пространстве.

Пример 8.3. Е = {3, 4, 5} Ì R; x_n= , (x_n) Ì E.

Подпоследовательность (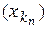 = (3, 3, …, 3…)) (n = 2 k)стремится к числу 3, если n®¥. Точка 3 принадлежит множеству ЕÌ R. Множество Е компакт в R.

Теорема 8.1. Если множество Е замкнуто в компактном метрическом пространстве (X, r), то оно компактно в этом пространстве [1, стр.29].

Изучим теперь некоторые свойства компактных множеств.

Теорема 8.2 (первое необходимое условие компактности). Если множество Е Ì Х компактно в метрическом пространстве (X, r), то оно замкнуто в этом пространстве.

3Пусть а – какая-нибудь предельная точка множества Е в метрическом пространстве (X, r). Поэтому можно выделить последовательность (x_n) Ì Е, которая сходится к а в этом пространстве (Т.5.4). Поскольку Е – компактное множество в метрическом пространстве (X, r), то существует подпоследовательность 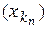Ì (x_n), которая сходится к точке а^*Î Е по метрике r: $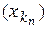 а^*Î Е. Известно, что подпоследовательность сходящейся последовательности сходится к тому же самому пределу. Таким образом а^*=а. Поскольку а^*Î Е, то и аÎ Е. 4

Пример 8.4. Интервал Е= (а, в)не является компактным множеством в пространстве R.

Теорема 8.3 (второе необходимое условие компактности). Если множество Е Ì Х компактно в метрическом пространстве (X, r), то оно ограничено в этом пространстве [1, стр.30-31].

Замечание 8.1. Теоремы, обратные теоремам 2 и 3, вообще говоря не имеют место в любом метрическом пространстве.

Теорема 8.4 (критерий компактности в R^m). Для того, чтобы множество ЕÌ R^m было компактным в метрическом пространстве R^m, необходимо и достаточно, чтобы оно было замкнутым и ограниченным в этом пространстве.

Доказательство необходимости следует из теорем 8.2 и 8.3.

3достаточности.

Рассмотрим произвольную последовательность (x_n) Ì Е. Поскольку множество Е ограничено в метрическом пространстве R^m по условию теоремы, то и последовательность (x_n) ограничена. Поэтому по теореме Больцано-Вейерштрасса из нее можно выделить подпоследовательность 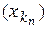, сходящуюся к некотому числу а. Это число является предельной точкой для последовательности 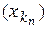Ì Е, а поэтому и для множества Е. В силу замкнутости множества ЕÌ Х, число аÎ Е, подпоследовательность 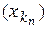сходится к числу аÌ Е, то множество Е компактно по определению (8.2).

Пример 8.5. Множество Е= [0, 1] È {5} Ì R – компактное множество.

Пример 8.6. Замкнутый шар в пространстве R^m – компактное множество.

Пример 8.7. Множество {1 /n, nÎ N } Ì R не будет компактным, поскольку оно не является замкнутым.