Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. 1. Если а > 0, то интеграл вида рационализируется подстановкой .
|
|
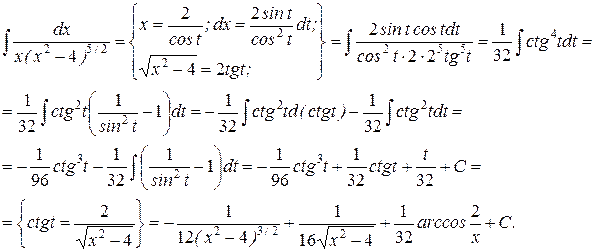
2. Подстановки Эйлера
1. Если а > 0, то интеграл вида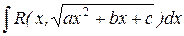 
рационализируется подстановкой 
.
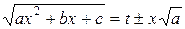2. Если a < 0 и c > 0, то интеграл вида 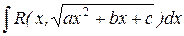рационализируется подстановкой 
.
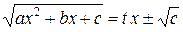3. Если a < 0, а подкоренное выражение раскладывается на действительные множители a (x – x1)(x – x2), то интеграл вида 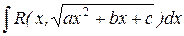рационализируется подстановкой 
.
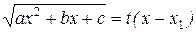Отметим, что подстановки Эйлера неудобны для практического использования, т.к. даже при несложных подынтегральных функциях приводят к весьма громоздким вычислениям.
3. Метод неопределенных коэффициентов.
Рассмотрим интегралы следующих трех типов:
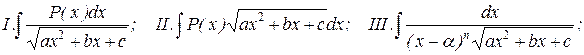
где P(x) – многочлен, n – натуральное число.
Причем интегралы II и III типов могут быть легко приведены к виду интеграла I типа.
Интегралы типа I можно вычислять, пользуясь формулой
,
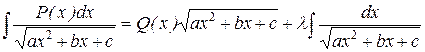где Q(x) - некоторый многочлен, степень которого ниже степени многочлена P(x), а l - некоторая постоянная величина.
Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируем обе части данного выражения, затем умножают на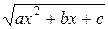 
и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).
Данный метод выгодно применять, если степень многочлена Р(х) больше единицы. В противном случае можно успешно использовать методы интегрирования рациональных дробей, рассмотренные выше, т.к. линейная функция является производной подкоренного выражения.
|
|