Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод подстановки (замены переменной)
|
|
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. При этом исходный интеграл приводится к новому интегралу, который является либо табличным, либо сводящимся к нему.
Если требуется найти интеграл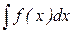 
и отыскание первообразной при этом вызывает затруднение, то часто оказывается удобным произвести замену переменной интегрирования, полагая x = j(t) и dx = j¢ (t)dt в результате получим:
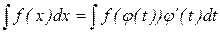
Примеры. Найти неопределенный интеграл:
1. 
.
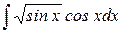Сделаем замену t = sinx, dt = cosxdt.
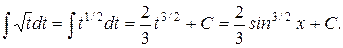
2. 
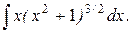
Замена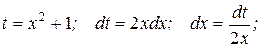 
Получаем:
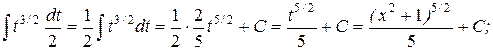
Интегрирование по частям.
Этот метод основан на известной формуле производной произведения:
(uv)¢ = u¢ v + v¢ u,
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: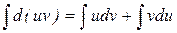 
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
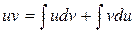или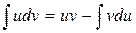 
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
|
|