
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Первообразная и неопределенный интеграл.
|
|
Определение. Функция F(x) называется первообразной функцией функции f(x) на отрезке [ a, b ], если в любой точке этого отрезка верно равенство:
F¢ (x) = f(x).
Надо отметить, что число первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Определение. Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением
F(x) + C.
Обозначение неопределённого интеграла -
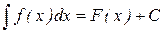 . (6.1)
. (6.1)
Здесь функция f(x) называется подынтегральной, f(x)dx –подынтегральным выражением, х – переменной интегрирования, 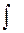 - обозначение операции интегрирования(оператор интегрирования)
- обозначение операции интегрирования(оператор интегрирования)
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства неопределённого интеграла
1. 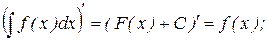
2. 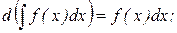
3. 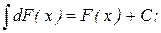
4. 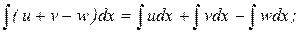 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 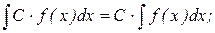
Пример: 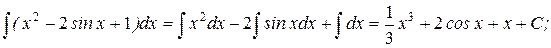
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций такая задача оказывается сложной, либо невозможной. В последнем случае имеется в виду, что первообразная функция не является элементарной. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Таблица основных неопределённых интегралов
Из определения первообразной функции следует, что интегрирование есть операция, обратная дифференцированию. Поэтому проверка правильности выполнения интегрировании я нужно продифференцировать результат и получить при этом подынтегральную функцию. Для удобства проведения интегрирования ниже приводится таблица основных неопределённых интегралов.
Таблица интегралов
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
| Интеграл | Значение | Интеграл | Значение | ||
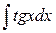
| -ln½ cosx½ + C | 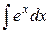
| ex + C | ||
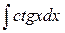
| ln½ sinx½ + C | 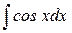
| sinx + C | ||
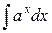
| 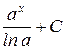
| 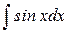
| -cosx + C | ||
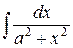
| 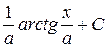
| 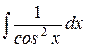
| tgx + C | ||
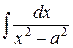
| 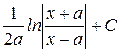
| 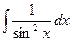
| -ctgx + C | ||
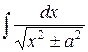
| ln 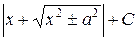
| 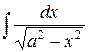
| arcsin 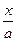 + C + C
| ||
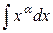
| 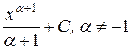
| 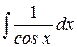
| 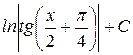
| ||
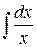
| 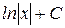
| 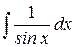
| 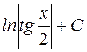
|
Интегралы этой таблицы принято называть табличными.
Если операции дифференцирования не выводит нас из области элементарных функций, т.е. результат дифференцирования также является элементарной функцией. С операцией интегрирования дело обстоит иначе: интегралы от некоторых элементарных функций уже не являются элементарными функциями. Приведём примеры некоторых из них:
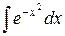 - интеграл Пуассона (интеграл ошибок);
- интеграл Пуассона (интеграл ошибок);
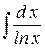 - интегральный логарифм;
- интегральный логарифм;
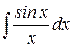 - интегральный синус.
- интегральный синус.
Приведенные интегралы принято называть «неберущимися». Каждый из этих интегралов не является элементарной функцией, однако они имеют большое значение в прикладной математике.
|
|
