Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. 2. Интегрирование дробно-рациональных функций
|
|
=
= 
= 
=
= 
.
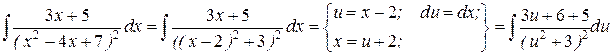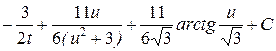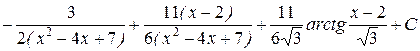2. Интегрирование дробно-рациональных функций. Отношение двух многочленов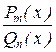 
(Pm(x) – многочлен степени m, а Qn(x) – многочлен степени n) – называется дробно-рациональной функцией (рациональной дробью).
Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. m < n, в противном случае рациональная дробь – неправильная.
Имеет место утверждение: всякую неправильную рациональную дробь путём деления числителя на знаменатель можно представит в виде суммы многочлена и правильной рациональной дроби, т.е.
Например,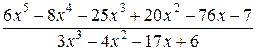 
- неправильная рациональная дробь. Разделим числитель на знаменатель
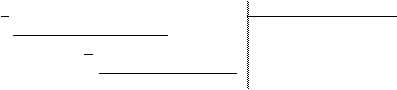6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
Получим частное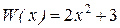 
и остаток 
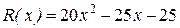. Поэтому
= 
+ 
.
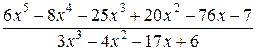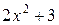Теорема. Если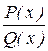 
- правильная рациональная дробь, знаменатель Q(x) которой представлен в виде произведения линейных и квадратичных множителей
Q(x) =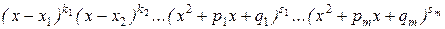 
,
то эта дробь может быть представлена в виде суммы простейших дробей:
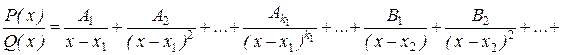
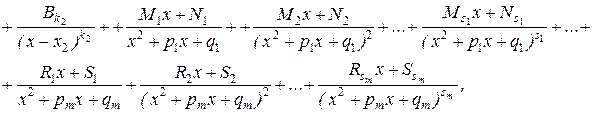
где Ai, A2, …, B1, B2, …, M1, N1, …, R1, S1, … – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Так как (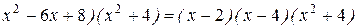
, то
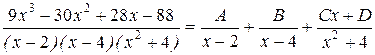
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
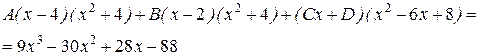
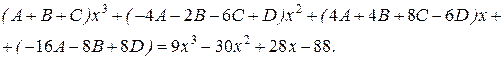
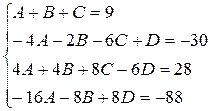
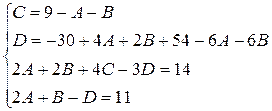
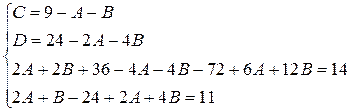
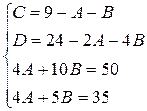
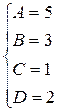
Таким образом,
|
|
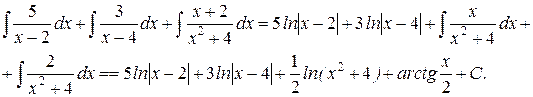