Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Простейший пуассоновский поток

На практике часто встречаются ситуации, где имеет место распределение Пуассона. Рассмотрим следующую задачу.

Пусть на оси времени 0 t случайным образом возникают точки – моменты появления каких-то однородных событий (например, вызовов на телефонной станции, приходов посетителей в магазин и т.п.). Последовательность таких моментов назовем «потоком событий». Предположим, что поток обладает следующими свойствами.

1. Стационарность. Это свойство означает, что вероятность попадания того или иного числа событий на участок времени длины 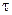не зависит от того, где на оси 0 t расположен этот участок, а зависит только от его длины 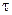. Из этого следует, что среднее число событий, появляющихся в единицу времени, постоянно. Обозначим его 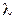, и будем называть интенсивностью потока.

2. Ординарность. Это свойство заключается в том, что вероятность попадания на малый участок 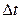двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события (т.е. при 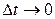вероятность попадания на участок 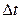более одного события есть бесконечно малая более высокого порядка малости, чем вероятность попадания на него же ровно одного события).

3. Отсутствие последействия. Это свойство означает, что вероятность попадания того или другого числа событий на заданный участок оси 0 t не зависит от того, сколько событий попало на любой другой не пересекающийся с ним участок (в частности, «будущее» потока не зависит от его «прошлого»; отсюда и термин – «отсутствие последействия»).

Определение. Поток событий, обладающий этими тремя свойствами (стационарностью, ординарностью и отсутствием последействия), называется простейшим (или стационарным) пуассоновским потоком.

Простейший пуассоновский поток тесно связан с распределением Пуассона:

.

Пример 2.1.30. На автоматическую телефонную станцию поступает простейший поток вызовов с интенсивностью 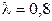(вызов/мин). Найти вероятность того, что за 2 минуты: а) не придет ни одного вызова; б) придет ровно один вызов; в) придет хотя бы один вызов.

Решение. Случайная величина Х – число вызовов за 2 минуты – распределена по закону Пуассона с параметром . Имеем:

а) 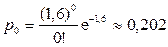; б) ;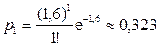

в) .

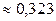Ответ: а) ; б) ; в) 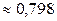.