
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 2.1.1. Функция распределения случайной величины X непрерывна
|
|
2.1.1. Функция распределения случайной величины X непрерывна. Может ли случайная величина X быть СВДТ?
2.1.2. Случайная величина X принимает два значения 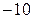 и 10 с вероятностями
и 10 с вероятностями  и
и 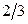 соответственно. Является ли она непрерывной случайной величиной?
соответственно. Является ли она непрерывной случайной величиной?
2.1.3. Случайная величина X принимает только два различных значения a (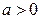 ) и
) и 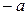 с вероятностями 0, 5. Верно ли, что: 1)
с вероятностями 0, 5. Верно ли, что: 1)  ; 2)
; 2) 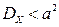 ?
?
2.1.4. Случайная величина X принимает только два различных значения 1 и 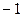 с вероятностями 0, 5. Вычислить
с вероятностями 0, 5. Вычислить 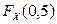 и
и 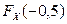 .
.
2.1.5. Функции 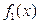 и
и  являются плотностями вероятности. Является ли функция
являются плотностями вероятности. Является ли функция 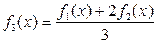 плотностью вероятности?
плотностью вероятности?
2.1.6. Функции 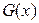 и
и 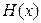 являются функциями распределений. Является ли функция
являются функциями распределений. Является ли функция 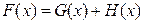 функцией распределения некоторой случайной величины?
функцией распределения некоторой случайной величины?
2.1.7. Баскетболист бросает мяч в корзину до первого попадания, но не более трех раз. Вероятность попадания при каждом броске равна 0, 8. Случайная величина X – количество произведенных бросков. Составить ряд распределения X. Найти математическое ожидание и дисперсию X. Составить функцию распределения  и построить ее график.
и построить ее график.
2.1.8. В урне 2 белых и 3 черных шара. Наудачу вынимаются два шара. Случайная величина X – число белых шаров среди вынутых. Составить ряд распределения X. Найти математическое ожидание и дисперсию X. Составить функцию распределения  и построить ее график.
и построить ее график.
2.1.9. На шахматную доску поставлен слон. СВДТ X – число клеток, которые стоят под ударом этого слона. Составить ряд распределения X. Найти математическое ожидание и дисперсию X. Составить функцию распределения  и построить ее график.
и построить ее график.
2.1.10. Дан ряд распределения СВДТ Х и известно, что 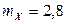 :
:
| X | ||||
| P | 0, 1 | 0, 2 | a | b |
Найти: числа а и b и дисперсию случайной величины X. Составить функцию распределения  и построить ее график.
и построить ее график.
2.1.11. В группе из 10 студентов, изучающих английский язык, 8 москвичей и 2 иногородних. Для социологического опроса случайным образом выбирают двух студентов из этой группы. Пусть X – число москвичей среди выбранных. Построить ряд распределения случайной величины X и найти ее математическое ожидание.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
2.1.12. Лотерея заключается в розыгрыше трех номеров из шести. Порядок выпадения выигрышных номеров неважен. Выигрыш при угадывании одного номера из трех составляет 20 рублей, двух номеров из трех – 100 рублей, всех трех номеров – 500 рублей. Найти средний выигрыш при покупке одного билета лотереи. Составить функцию распределения размера выигрыша.
2.1.13. СВНТ Х имеет плотность распределения
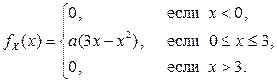
Найти: коэффициент а, математическое ожидание, моду, медиану и дисперсию X. Составить функцию распределения  .
.
2.1.14. СВНТ Х имеет плотность распределения
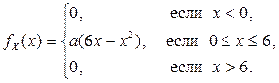
Найти: коэффициент а, математическое ожидание, моду, медиану и дисперсию X. Составить функцию распределения  .
.
2.1.15. Случайная величина имеет функцию распределения
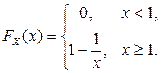
Найти a, для которого 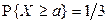 .
.
Ответы к упражнениям
2.1.1. Нет.
2.1.2. Нет.
2.1.3. 1) неверно; 2) неверно.
2.1.4. 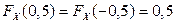 .
.
2.1.5. Является.
2.1.6. Не является.
2.1.7.
| Х | |||
| P | 0, 8 | 0, 16 | 0, 04 |
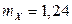 ,
,  ,
, 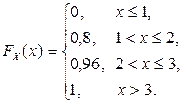
2.1.8.
| Х | |||
| P | 0, 3 | 0, 6 | 0, 1 |
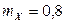 ,
,  ,
, 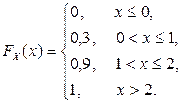
2.1.9.
| Х | ||||
| P | 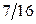
| 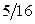
| 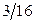
| 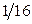
|
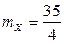 ,
,  ,
, 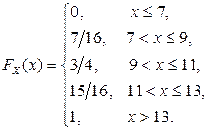
2.1.10.
| Х | ||||
| P | 0, 1 | 0, 2 | 0, 5 | 0, 2 |
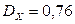 ,
, 
2.1.11. 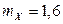 ,
,
| Х | |||
| P | 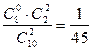
| 
| 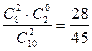
|
Указание. Эта задача на гипергеометрическое распределение (пример 2.1.4), причем роль белых шаров играют москвичи.
2.1.12. Средний выигрыш составляет 79 рублей,
| Х | ||||
| P | 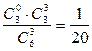
| 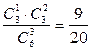
| 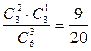
| 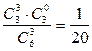
|
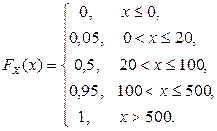
2.1.13. 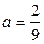 ,
, 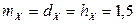 ,
,  ,
, 
2.1.14. 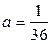 ,
, 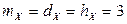 ,
, 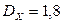 ,
, 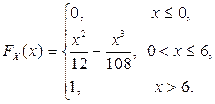
2.1.15. 3.
|
|
