Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Биномиальное распределение. Определение. СВДТ Х имеет биномиальное распределение, если ее возможные значения (реализации) , где

Определение. СВДТ Х имеет биномиальное распределение, если ее возможные значения (реализации) 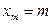, где 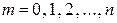, а соответствующие им вероятности:

,

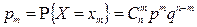где ; .

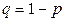Замечание. Это распределение зависит от двух параметров – n и p, поэтому пишут .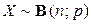

На практике биномиальное распределение возникает при следующих условиях. Пусть производится n независимых опытов (испытаний), в каждом из которых событие А (условно можно назвать его «успехом» опыта) появляется с вероятностью p, случайная величина Х – число «успехов» при n опытах.

Замечание. Опыты (испытания) называются независимыми, если вероятность какого-либо исхода каждого из них не зависит от того, какие исходы имели другие опыты.

Важнейшие числовые характеристики :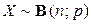

, , .

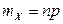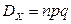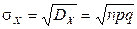Наиболее вероятное значение, т.е. мода , случайной величины 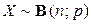удовлетворяет неравенству

.

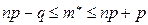Пример 2.1.26. Передается 5 сообщений по каналу связи (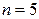). Каждое сообщение с вероятностью 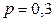, независимо от других искажается. Случайная величина Х – количество искаженных сообщений. Построить ряд распределения; найти 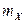, , 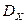, , 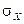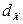а также вероятность того, что будет искажено не менее двух сообщений.

Решение. СВДТ X – количество искаженных сообщений – имеет биномиальное распределение с параметрам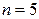и и 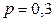. Ряд распределения СВДТ X имеет вид:

X
P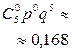

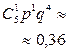
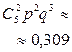
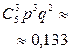
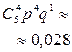
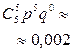
Тогда: 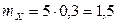, , 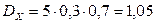, 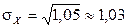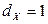(это следует как из ряда распределения, так и из неравенства );

.

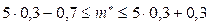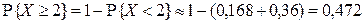Ответ: , , , , .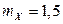

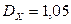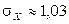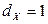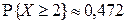Пример 2.1.27. Вероятность того, что при трех независимых выстрелах стрелок попадет в цель хотя бы один раз, равна 0, 992. Найти математическое ожидание, дисперсию и моду числа попаданий при двадцати выстрелах.

Решение. СВДТ X – количество попаданий в цель при трех выстрелах – имеет биномиальное распределение с параметрами и p, где вероятность p попадания при одном выстреле неизвестна. По условию задачи

.

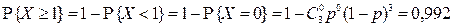Имеем уравнение: 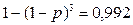, или 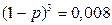. Отсюда 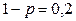, или .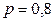

СВДТ Y – количество попаданий в цель при двадцати выстрелах – имеет биномиальное распределение с параметрам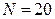и и 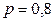, где вероятность p попадания в цель при одном выстреле (поскольку стрелок тот же, вероятность его попадания в цель та же, что и при трех выстрелах).

Поэтому математическое ожидание и дисперсия СВДТ Y равны соответственно: , .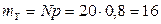

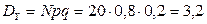Для нахождения моды воспользуемся неравенством 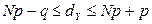. Тогда 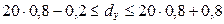, или 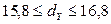. Значит, .

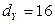Ответ: 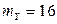, , .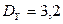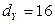