
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывные случайные величины. Рассмотрим случай, когда множество возможных значений случайной величины несчетно.
|
|
Рассмотрим случай, когда множество возможных значений случайной величины несчетно.
Определение. Случайная величина X с непрерывной функцией распределения 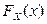 называется непрерывной случайной величиной.
называется непрерывной случайной величиной.
Определение. Плотностью распределения (плотностью вероятности) случайной величины X называется неотрицательная кусочно-непрерывная функция 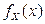 , для которой при любом
, для которой при любом 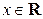 выполняется соотношение
выполняется соотношение
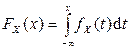 .
.
Определение. Случайная величина, у которой существует плотность вероятности, называется абсолютно непрерывной, или случайной величиной непрерывного типа (сокращенно СВНТ).
Замечание. Кроме абсолютно непрерывных случайных величин существуют непрерывные случайные величины, называемые сингулярными, которые не имеют плотности вероятности. В дальнейшем такие случайные величины не рассматриваются.
Покажем, что для СВНТ X 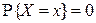 для произвольного фиксированного
для произвольного фиксированного 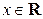 . Действительно, из равенства
. Действительно, из равенства
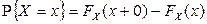 ,
,
равносильного
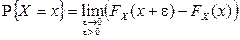 ,
,
следует, что вероятность «попасть в точку» для СВНТ X равна нулю.
Из определения следуют свойства плотности распределения 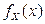 :
:
1. 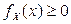 для всех
для всех 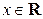 (условие неотрицательности плотности).
(условие неотрицательности плотности).
2. 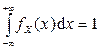 (условие нормировки плотности).
(условие нормировки плотности).
3. 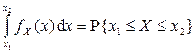
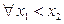 .
.
Замечание. Таким образом, через плотность вероятности 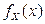 можно вычислить вероятность
можно вычислить вероятность 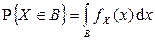 для любого
для любого 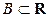 .
.
4. 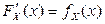 в точках непрерывности плотности
в точках непрерывности плотности 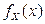 .
.
Пример 2.1.10. Даны функции:
 ,
, 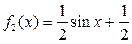 ,
,  .
.
Являются ли эти функции плотностями вероятности?
Решение. Для функции  не выполнено условие неотрицательности, т.к.
не выполнено условие неотрицательности, т.к. 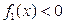 для всех
для всех  . Для функции
. Для функции 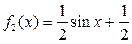 не выполнено условие нормировки, т.к. интеграл
не выполнено условие нормировки, т.к. интеграл  расходится. Наконец, для функции
расходится. Наконец, для функции  выполнены условия неотрицательности и нормировки, поскольку, очевидно,
выполнены условия неотрицательности и нормировки, поскольку, очевидно,  для всех действительных x и
для всех действительных x и
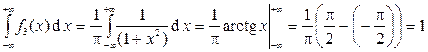 .
.
Ответ: плотностью распределения является только 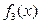 .
.
Пример 2.1.11. СВНТ X задана функцией распределения
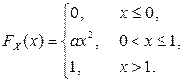
Найти: 1) коэффициент a; 2) 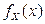 и построить ее график; 3)
и построить ее график; 3)  .
.
Решение. 1) Так как 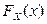 непрерывна, то
непрерывна, то  , т.е.
, т.е. 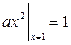 . Отсюда
. Отсюда 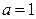 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 2) Плотность распределения
2) Плотность распределения 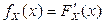 . Поэтому функция плотности
. Поэтому функция плотности 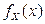 :
:

График плотности 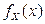 приведен на рис. 2.1.4.
приведен на рис. 2.1.4.
3) 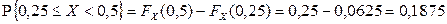 .
.
Ответ: 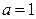 ,
,  ,
, 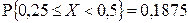 .
.
Пример 2.1.12. СВНТ X задана функцией плотности

Найти: 1) коэффициент a; 2) 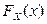 и построить ее график; 3)
и построить ее график; 3)  .
.
Решение. 1)  . Отсюда
. Отсюда 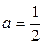 .
.
2) По определению  .
.
Пусть  , тогда
, тогда 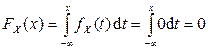 .
.
Пусть  , тогда
, тогда
 .
.
Пусть 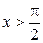 , тогда
, тогда 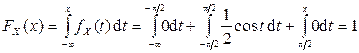 .
.
 Таким образом, функция распределения
Таким образом, функция распределения 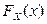 :
:
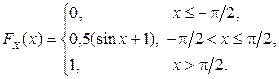
График функции распределения 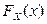 приведен на рис. 2.1.5.
приведен на рис. 2.1.5.
3) 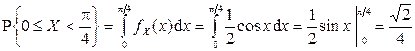 .
.
Ответ:  .
.
|
|
