
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные формулы по физике
⇐ ПредыдущаяСтр 60 из 60
|
|
V= 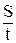 Vср.=
Vср.= 
| при равномерном движении скорость V равна отношению пути S ко времени t.
Vср. - средняя скорость равна отношению пути  S к промежутку времени S к промежутку времени  t, в течение которого этот путь был пройден. t, в течение которого этот путь был пройден.
|
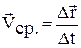
|  - вектор средней скорости перемещения за время - вектор средней скорости перемещения за время  t, t, 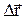 - вектор перемещения. - вектор перемещения.
|
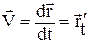
| 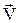 - вектор мгновенной скорости равен производной от перемещения по времени. - вектор мгновенной скорости равен производной от перемещения по времени.
|
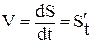
| V - модуль мгновенной скорости равен производной от пути по времени. |

|  - вектор среднего ускорения равен отношению изменения скорости - вектор среднего ускорения равен отношению изменения скорости 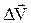 к промежутку времени к промежутку времени  , за которое это изменение произошло. , за которое это изменение произошло.
|
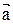 = = 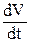 =Vt¢ =Vt¢
| мгновенное ускорение равно производной от скорости по времени |

| тангенциальное (касательное) ускорение характеризует быстроту изменения скорости по модулю и направлено по касательной к траектории в данной точке. |

| нормальное (центростремительное) ускорение аn характеризует быстроту изменения скорости по направлению и направлено к центру кривизны траектории. R - радиус кривизны траектории, V-скорость. (при равномерном вращении по окружности аn-центростремительное ускорение, R-радиус окружности). |
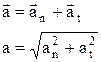
| а-полное ускорение при криволинейном движении; an, at-нормальное (центростремительное) и тангенциальное (касательное) ускорения, соответственно. |
| х(t)=x0 + V0 . t | кинематическое уравнение равномерного движения вдоль оси х, x0 - начальная координата, t - время. |
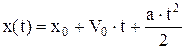
| кинематическое уравнение равнопеременного движения (а=const) вдоль оси х, V0 - начальная скорость. Значения V0 и а - положительны, если векторы  и и 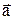 направлены в сторону положительной полуоси х, и отрицательны в противном случае. направлены в сторону положительной полуоси х, и отрицательны в противном случае.
|
S=V0t + 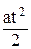 V=V0 + a . t
V=V0 + a . t
| S-путь и V-мгновенная скорость при равнопеременном движении, V0 - начальная скорость, а - ускорение, t - время. |
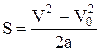
| кинематическое уравнение, связывающее путь S, пройденный телом за некоторое время, с начальной - V0 и конечной - V скоростями на этом отрезке пути, с ускорением а. |
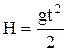 ; ; 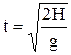 h(t)=H-
h(t)=H- 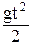
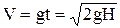
| свободное падение (v0 = 0) тела с высоты Н: t - время падения; g - ускорение свободного падения; V -скорость тела в момент достижения поверхности (Земли), h(t) – высота в момент времени t. |
х(t)=V0× t;
 ; ;
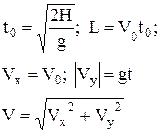
| движение тела, брошенного горизонтально со скоростью V0 с высоты Н: х0 = 0 и у0 = Н - начальное положение тела (в момент броска); х(t) и у(t) - уравнения движения по осям; t0 - время полета; L - дальность полета; Vx и Vy - составляющие скорости  тела по осям координат для любого момента времени t во время полета (до удара о поверхность). тела по осям координат для любого момента времени t во время полета (до удара о поверхность).
|
Vox = V0 × cosa; V0у = V0 × sina;
x(t)=Vox(t); y(t)=Voy× t- 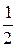 gt2; Vx(t)=Vox; Vy(t) = Voy - gt;
H= gt2; Vx(t)=Vox; Vy(t) = Voy - gt;
H=  ; t0 = ; t0 = 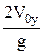 ;
L = ;
L = 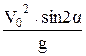
| движение тела, брошенного со скоростью V0 под углом a к горизонту: х0 = 0 и у0 = 0 - начальное положение тела (в момент броска); Vox и Voy - проекции скорости 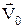 по осям; х(t) и у(t) - уравнения движения по осям; Vx(t) и Vy(t)- зависимость составляющих скорости по осям от времени t; Н - высота подъема, t0 - время полета; L - дальность полета по осям; х(t) и у(t) - уравнения движения по осям; Vx(t) и Vy(t)- зависимость составляющих скорости по осям от времени t; Н - высота подъема, t0 - время полета; L - дальность полета
|
n= 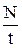 , ,  n=T-1, T=n-1
n=T-1, T=n-1
| при равномерном вращательном движении: n - частота вращения, Т - период вращения, N - число оборотов за время t. |
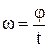 ; N= ; N= 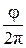 ; w=2pn= ; w=2pn= 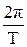
| w - угловая скорость при равномерном вращении: j - угол поворота, N - число оборотов за время t; n - частота вращения, Т - период вращения. |

| w - угловая скорость равна производной угла поворота по времени. |
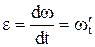
| e - угловое ускорение равно производной угловой скорости по времени. |
| S=R . j | S - путь, пройденный материальной точкой при повороте на угол j по дуге окружности радиуса R. |
V=w . R= 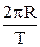 =2pRn =2pRn
| связь между линейной и угловой скоростями при равномерном вращательном движении |
at=R× e, an=w2 . R= 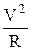 =V . w =V . w
| an и at - нормальное (центростремительное) и тангенциальное (касательное) ускорения, соответственно. |
| j(t)=j0 + w0 . t | кинематическое уравнение равномерного вращения, j0 - начальное угловое положение. |
j(t)=j0 + w0 . t + 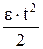
| кинематическое уравнение равнопеременного вращения (e=const), w0 - начальная угловая скорость. |
w(t)= w0 + e . t
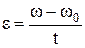
| w - мгновенная угловая скорость при равнопеременном вращении в момент времени t, w0 - начальная угловая скорость, e - угловое ускорение. |
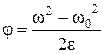
| кинематическое уравнение, связывающее угол поворота j с начальной w0 и конечной w угловыми скоростями и с угловым ускорением e. |
r= 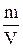
| r- плотность тела, m - масса, V - объем тела. |
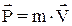
| 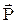 - импульс тела - векторная величина, равная произведению массы тела на его скорость - импульс тела - векторная величина, равная произведению массы тела на его скорость  . .
|

| второй закон Ньютона: m - масса тела,   - равнодействующая всех приложенных к телу сил, - равнодействующая всех приложенных к телу сил,  - ускорение, - ускорение, 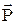 - импульс тела. - импульс тела.
|
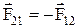
| третий закон Ньютона: силы, с которыми действуют друг на друга два тела, всегда равны по модулю и противоположно направлены. |
 ,
s=e . Е, ,
s=e . Е,
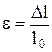 , , 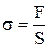 Dl = l - l0
Dl = l - l0
| закон Гука: сила упругости Fупр. пропорциональна удлинению тела (пружины) 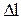 и направлена в сторону, противоположную направлению перемещений частиц тела при деформации; k - коэффициент пропорциональности (жесткость пружины); s - механическое напряжение; S - площадь поперечного сечения образца, к которому приложена сила F; Е - модуль Юнга (упругости); e - относительное удлинение; l0 - начальная длина. и направлена в сторону, противоположную направлению перемещений частиц тела при деформации; k - коэффициент пропорциональности (жесткость пружины); s - механическое напряжение; S - площадь поперечного сечения образца, к которому приложена сила F; Е - модуль Юнга (упругости); e - относительное удлинение; l0 - начальная длина.
|

| закон всемирного тяготения: два тела притягиваются друг к другу с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния R между их центрами масс; G - гравитационная постоянная. В такой форме записи закон справедлив для взаимодействия материальных точек и однородных тел сферической формы. |
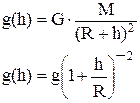
| g(h) - ускорение свободного падения на высоте h над поверхностью планеты, M и R - масса и радиус планеты; g - ускорение свободного падения у поверхности планеты (без учета вращения планеты), т.е.  . .
|
| Fтр.=m . N | сила трения скольжения равна максимальной силе трения покоя Fтр., пропорциональной силе нормального давления N (реакции опоры); m - коэффициент трения. |

| P - сила тяжести, m - масса тела, g - ускорение свободного падения. |
 = = 
| V1 - первая космическая скорость: M и R - масса и радиус планеты, G - гравитационная постоянная, g - ускорение свободного падения на поверхности планеты. |
V2= 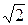 V1= V1= 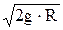
| V2 – вторая космическая скорость, V1 - первая космическая скорость. |
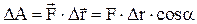
|  А - элементарная работа равна скалярному произведению силы А - элементарная работа равна скалярному произведению силы  на перемещение на перемещение 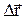 , a - угол между , a - угол между  и и 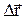 . .
|
Nср.= 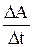
| мощность равна работе, совершаемой в единицу времени: Nср - средняя мощность за время Dt. |

| мгновенная мощность N равна скалярному произ-ведению силы  на скорость на скорость 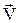 , с которой движется точка приложения силы, a - угол между , с которой движется точка приложения силы, a - угол между  и и 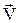 . .
|
EК= 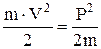
| EК - кинетическая энергия тела массой m, движущегося со скоростью V, P - импульс тела. |
| А=ЕК2 - ЕК1 | работа равнодействующей силы равна изменению кинетической энергии тела (при условии постоянства потенциальной энергии). |
А= 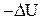
| работа консервативных сил совершается за счет убыли потенциальной энергии (при условии постоянства кинетической энергии). |
| ЕП=m g . h | потенциальная энергия тела в однородном поле тяготения: h - высота над поверхностью Земли (высота от нулевого уровня), g - ускорение свободного падения, m - масса тела. |
ЕП= 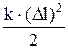
| потенциальная энергия упруго деформированного тела (пружины). |
ЕП= 
| потенциальная энергия взаимодействия двух тел массами m1 и m2, находящихся на расстоянии R друг от друга. |
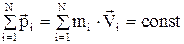
| закон сохранения импульса: суммарный импульс замкнутой системы остается постоянным (по величине и направлению) при любых взаимодействиях тел этой системы между собой. |
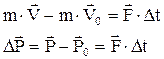
| изменение импульса тела 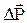 за время за время  равно импульсу равнодействующей силы равно импульсу равнодействующей силы 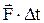 . .
|
| Е=EK + EП | полная механическая энергия материальной точки (тела) равна сумме кинетической и потенциальной энергий. |
| Е=EK + EП=сonst | закон сохранения полной механической энергии: полная механическая энергия замкнутой системы тел остается постоянной при любых движениях тел системы, если в системе не действуют диссипативные силы. |

| законы сохранения импульса и энергии при центральном абсолютно упругом ударе двух тел (шаров). |
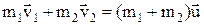
| закон сохранения импульса при центральном абсолютно неупругом ударе двух тел. |
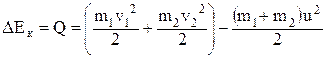
| изменение кинетической энергии при абсолютно неупругом ударе (часть ее переходит в «тепловую» форму энергии). |
h= 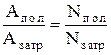 h=
h= 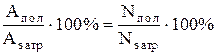
| коэффициент полезного действия механизмов равен отношению полезной работы Aпол (полезной мощности Nпол) к затраченной Aзатр (затраченной - Nзатр). | |
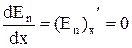
| условие равновесия - экстремальное значение потенциальной энергии (для случая одномерной задачи, когда Еп зависит только от координаты х, т.е. когда Еп = Еп(х)). | |
 > 0 > 0
| условие устойчивого равновесия |
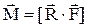
| момент силы 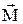 относительно неподвижной точки - физическая величина, равная векторному произведению радиус-вектора относительно неподвижной точки - физическая величина, равная векторному произведению радиус-вектора 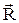 , проведенного из этой точки в точку приложения силы, на эту силу , проведенного из этой точки в точку приложения силы, на эту силу  . .
|
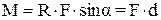
| модуль момента силы - M, a - угол между 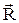 и и  ,
d=R. sina - плечо силы равно кратчайшему расстоянию от оси вращения до линии действия силы. ,
d=R. sina - плечо силы равно кратчайшему расстоянию от оси вращения до линии действия силы.
|
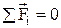
| (первое) условие равновесия тела при отсутствии вращения: векторная сумма всех сил, приложенных к телу, равна нулю. |

| (второе) условие равновесия твердого тела с неподвижной осью вращения: алгебраическая сумма моментов сил относительно любой оси равна нулю, причем моменты сил, вращающих в одну сторону, считают положительными, а в другую - отрицательными. |

| центр тяжести тела: сумма моментов сил тяжести всех частиц тела по отношению к оси, проходящей через центр тяжести, равна нулю. |
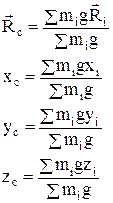
| центр тяжести тела:  - радиус-вектор, проведенный из начала координат в центр тяжести тела; xc, yc, zc - координаты центра тяжести; xi, yi, zi - координаты частиц тела, причем - радиус-вектор, проведенный из начала координат в центр тяжести тела; xc, yc, zc - координаты центра тяжести; xi, yi, zi - координаты частиц тела, причем 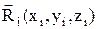 ; суммирование производится по всем частицам тела. ; суммирование производится по всем частицам тела.
|
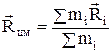
|  (хцм, уцм, zцм) - радиус-вектор центра масс системы материальных точек; mi и (хцм, уцм, zцм) - радиус-вектор центра масс системы материальных точек; mi и  - масса и радиус-вектор i-ой материальной точки (если твердое тело, то суммирование производится по всем частицам тела). - масса и радиус-вектор i-ой материальной точки (если твердое тело, то суммирование производится по всем частицам тела).
|

| координаты центра масс и центра тяжести тела совпадают в случае, если размерами тела можно пренебречь в сравнении с размерами Земли (планеты). |
| М = F× d | момент пары сил: d- плечо пары сил (F1=F2=F) – кратчайшее расстояние между линиями действия сил. |
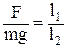
| правило рычага: во сколько раз плечо l2 силы F больше плеча l1 груза весом mg, тем меньше усилие F требуется, чтобы сдвинуть груз. |
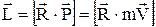 L=R× P× sina=P× d
L=R× P× sina=P× d
| 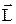 -момент импульса материальной точки относительно неподвижной точки О: -момент импульса материальной точки относительно неподвижной точки О: 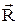 -радиус-вектор от точки О до материальной точки; -радиус-вектор от точки О до материальной точки;  - импульс материальной точки; a - угол между - импульс материальной точки; a - угол между 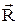 и и 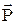 ; d - плечо вектора ; d - плечо вектора 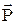 относительно неподвижной точки О. относительно неподвижной точки О.
|
P= 
| давление равно отношению силы, перпендикулярной к поверхности тела, к величине площади поверхности S, на которую действует эта сила. |
| P=r . g . h | P - гидростатическое давление: r - плотность жидкости, h - высота столба жидкости, g - ускорение свободного падения. |
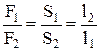
| гидравлический пресс дает выигрыш в силе во столько раз, во сколько раз площадь ее большого поршня превосходит площадь маленького поршня, S1 и S2 - площади поперечного сечения поршней, l1 и l2 - перемещения поршней, F1 и F2 - силы, приложенные к поршням. |
| FA=r . g . Vп | закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом жидкости или газа. r - плотность жидкости (газа), Vп - объем погруженной в жидкость (газ) части тела, g - ускорение свободного падения. |
| S . v=const | уравнение неразрывности (непрерывности) для несжимаемой жидкости: произведение скорости течения v на поперечное сечение S трубки тока есть величина постоянная для данной трубки тока; |
| V=S× v× t | объем жидкости (газа) V, проходящий через сечение S струи (трубы) за время t. |
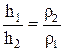
| в сообщающихся сосудах высота столбиков жидкостей над уровнем раздела обратно пропорциональна плотностям жидкостей. |
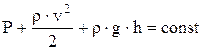
| уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости: Р - статическое давление, 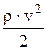 -динамическое давление, r . g . h - гидростатическое давление, v - скорость течения жидкости в данном сечении. -динамическое давление, r . g . h - гидростатическое давление, v - скорость течения жидкости в данном сечении.
| |
v= 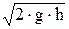
| формула Торричелли: v - скорость истечения жидкости из малого отверстия в открытом широком сосуде, h - глубина, на которой находится отверстие относительно уровня жидкости. | |
n= 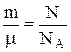
| n - количество вещества: m - молярная масса, NA - число Авогадро, N - число молекул в веществе (газе) массой m. |
m0= 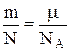
| m0 - масса одной молекулы. |
| T=t+273 | T - температура по абсолютной шкале температур (шкале Кельвина), t - температура по шкале Цельсия. |
| P . V=const | закон Бойля-Мариотта: для данной массы газа (m=const) при неизменности состава газа (молярная масса m=const) при постоянной температуре (T=const) произведение давления газа P на его объем V есть величина постоянная. |
V=V0. (1+at)
V= V0. a. T
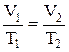
| закон Гей-Люссака: объем данной массы газа (m=const) при неизменности состава газа (молярная масса m=const) при постоянном давлении (Р=const) изменяется линейно с температурой, a=273-1 K-1 - термический коэффициент расширения, V0 - объем при 0 0С. |
P=P0.(1+bt)
P=P0.b. Т
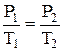
| закон Шарля: давление данной массы газа (m=const) при неизменности состава газа (молярная масса m=const) при постоянном объеме (V=const) изменяется линейно с температурой, b=273-1 K-1 - термический коэффициент давления, P0 - давление при 0 °С. |
Vm=  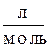
| закон Авогадро: моли любых идеальных газов при одинаковых условиях (одинаковых температуре и давлении) занимают одинаковые объемы, в частности, при нормальных условиях, - 22, 41 л. |
| P=760 мм рт. ст. t=0 °C | значения давления и температуры при нормальных условиях. |
| P=SPi | закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов; Pi - парциальное давление i-ой компоненты равно давлению, которое создавала бы i-ая компонента смеси газов, если бы она одна занимала объем, равный объему смеси при той же температуре. |
 =const =const
| уравнение Клапейрона справедливо при неизменности состава и массы газа, Р - давление, V - объем, Т - абсолютная температура. |
P . V= 
| уравнение Клапейрона-Менделеева (уравнение состояния идеального газа), m - масса газа, R - универсальная газовая постоянная, m - молярная масса газа. | |
| R=k . NA | R - универсальная газовая постоянная, k - постоянная Больцмана, NA - число Авогадро. | |
n=  ;
r = ;
r = 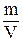 ; r=m0× n ; r=m0× n
| n - концентрация молекул - число молекул в единице объема. r -плотность газа, m0-масса одной молекулы |
| Р=n . k . T | зависимость давления Р от концентрации молекул n и температуры T; k - постоянная Больцмана. |
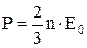 ;
Е0 = ;
Е0 = 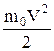
| основное уравнение молекулярно-кинетической теории идеальных газов: давление P идеального газа равно 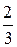 среднеквадратической кинетической энергии молекул, содержащихся в единице объема, m0 - масса одной молекулы, n - концентрация молекул. среднеквадратической кинетической энергии молекул, содержащихся в единице объема, m0 - масса одной молекулы, n - концентрация молекул.
|
E0= 
| E0 - среднеквадратическая кинетическая энергия поступательного движения молекулы идеального газа, m0 - масса молекулы, k - постоянная Больцмана, Т - температура, V – среднеквадратическая скорость. |
V = 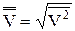 = = 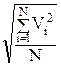
| V 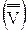 - среднеквадратическая скорость молекул идеального газа. - среднеквадратическая скорость молекул идеального газа.
|
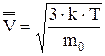 = =  = = 
| R - универсальная газовая постоянная, m - молярная масса, T - температура, P - давление, r - плотность газа, к- постоянная Больцмана, m0 - масса молекулы. |
Vср= 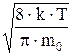 = = 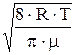 = = 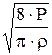
| Vср - средняя арифметическая скорость молекул газа. |
VН= 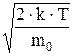 = = 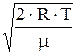 = = 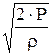
| VН - наиболее вероятная скорость молекул газа. |
l= 
| l - средняя длина свободного пробега молекул газа равна среднему расстоянию между двумя последовательными столкновениями молекулы, Z - среднее число соударений молекулы за 1 с, d - эффективный диаметр молекулы, n - концентрация молекул, Vср - относительная средняя арифметическая скорость молекул. |
Еср= 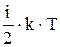
| Еср - средняя энергия молекулы, i - число степеней свободы молекул газа, k - постоянная Больцмана, T - температура. |
U= 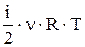
| U - внутренняя энергия идеального газа, n - количество вещества, R - универсальная газовая постоянная, T - температура. |
Q= 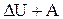
| первое начало термодинамики: количество теплоты Q, переданное системе, идет на изменение внутренней энергии 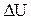 системы и на совершение системой работы A против внешних сил. системы и на совершение системой работы A против внешних сил.
|
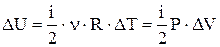
| 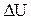 - изменение внутренней энергии при изменении температуры на - изменение внутренней энергии при изменении температуры на  ; DV-изменение объема при давлении Р. ; DV-изменение объема при давлении Р.
|
С= 
| С - теплоемкость численно равна количеству теплоты, необходимому для изменения температуры тела на 1 К. |
с= 
| с - удельная теплоемкость равна теплоемкости единицы массы тела, m - масса тела. |
СV= 
| СV - молярная теплоемкость газа при постоянном объеме, i - число степеней свободы молекул газа, R - универсальная газовая постоянная. |
СP= 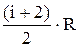
| СP - молярная теплоемкость газа при постоянном давлении. |
| R= СP - СV | уравнение Майера: универсальная газовая постоянная численно равна работе, которую 1 моль идеального газа совершает, изобарически расширяясь при нагревании на 1 К. |
А= 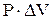
| А - работа, совершаемая газом при изменении его объема, Р - давление газа, 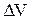 - изменение его объема. - изменение его объема.
|
А= 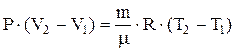
| A - работа газа при изобарическом процессе. |
А= 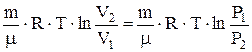
| A - работа газа при изотермическом процессе. |
А= 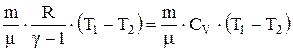
| A - работа газа при адиабатическом процессе, g - показатель адиабаты. |
 
| уравнение Пуассона (уравнение адиабатического процесса), g= 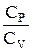 - показатель адиабаты. - показатель адиабаты.
|
g= 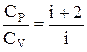
| g - показатель адиабаты, СP и СV - молярные теплоемкости при постоянных давлении и объеме, соответственно; i - число степеней свободы молекул газа. |
L=L0 . (1+a.t)
a= 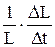 DL=L - L0
DL=L - L0
| линейное расширение твердых тел: L0 - длина при 0 °С, L - длина при температуре t °С, a - линейный коэффициент расширения равен относительному изменению длины при нагреве на 1 °С (1 К). |
V=V0 . (1+b.t)
b= 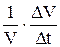 DV = V - V0
DV = V - V0
| объемное расширение твердых тел и жидкостей: V0 - объем при 0 °С, V - объем при температуре t °С, b - объемный коэффициент расширения равен относительному изменению объема при нагреве на 1 °С (1К). |
| b=3a | соотношение между коэффициентами линейного (a) и объемного (b) расширения твердых тел. |
q= 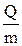
| удельная теплота сгорания равна количеству теплоты, выделяющемуся при сгорании единицы массы топлива. |
l= 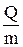
| количество теплоты, необходимое для превращения единицы массы из твердого (жидкого) состояния в жидкое (твердое) при температуре плавления (кристаллизации), называют удельной теплотой плавления (кристаллизации) l. Удельная теплота плавления равна удельной теплоте кристаллизации. Температура плавления равна температуре кристаллизации. |
r= 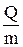
| количество теплоты, которое необходимо сообщить жидкости для испарения единицы ее массы при постоянной температуре (в частности, при температуре кипения), называют удельной теплотой парообразования r. С ростом температуры величина удельной теплоты парообразования уменьшается. |
h= 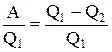
| h - коэффициент полезного действия теплового двигателя: A - работа, совершенная за цикл, Q1 - количество теплоты, полученное системой (от нагревателя), Q2 - количество теплоты, отданное системой (холодильнику; окружающей среде). |
h= 
| h - коэффициент полезного действия идеального теплового двигателя (цикла Карно): Т1 и Т2 - температуры нагревателя и холодильника, соответственно; Q1 - количество теплоты, полученное газом от нагревателя при изотермическом расширении; Q2 - количество теплоты, отданное газом холодильнику при изотермическом сжатии. |
r= 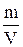
| абсолютной влажностью r называют количество водяного пара в граммах, содержащегося в 1 м3 воздуха при данной температуре. |
j= 
| относительной влажностью j называют отношение абсолютной влажности к тому количеству водяного пара, которое необходимо для насыщения 1 м3 воздуха при той же температуре. |
j= 
| относительной влажностью j называют отношение парциального давления Р водяного пара, содержащегося в воздухе при данной температуре, к давлению РН насыщенного пара при той же температуре. |
d= 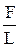
| d - коэффициент поверхностного натяжения равен силе поверхностного натяжения, приходящейся на единицу длины границы свободной поверхности жидкости. |
d= 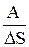
| d - коэффициент поверхностного натяжения равен работе, необходимой для увеличения свободной поверхности жидкости при постоянной температуре на единицу. |

| формула Лапласа: избыточное давление DР, обусловленное кривизной поверхности жидкости; r1 и r2 - радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; d - коэффициент поверхностного натяжения жидкости. |
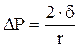
| избыточное давление в случае сферы: r – радиус сферы, d - коэффициент поверхностного натяжения. |
h= 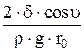
| h - высота подъема жидкости в капиллярной трубке: u - краевой угол, r0 - радиус капилляра, r - плотность жидкости, g - ускорение свободного падения, d - коэффициент поверхностного натяжения, (u = 0 - полное смачивание; u = 1800 - полное несмачивание) |
| Sqi= const | закон сохранения заряда: алгебраическая сумма зарядов в замкнутой системе (т.е. в системе, не обменивающейся зарядами с внешними телами) остается неизменной при любых процессах внутри этой системы. |
F= 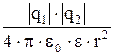 F = k
F = k 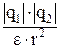
| закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами прямо пропорциональна абсолютным значениям зарядов и обратно пропорциональна квадрату расстояния между ними, e0-электрическая постоянная, k= 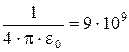 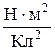 , e - диэлектрическая проницаемость изотропной непрерывной среды нахождения зарядов. , e - диэлектрическая проницаемость изотропной непрерывной среды нахождения зарядов.
| |
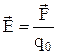
| 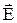 - напряженность электростатического поля равна силе, действующей на единичный положительный заряд, помещенный в данную точку поля. - напряженность электростатического поля равна силе, действующей на единичный положительный заряд, помещенный в данную точку поля.
| |
Е= 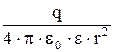
| Е - напряженность электростатического поля точечного заряда q на расстоянии r от него: e0 - электрическая постоянная, e - диэлектрическая проницаемость среды. | |
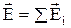
| принцип суперпозиции (наложения) электростатических полей: напряженность 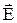 результирующего поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности. результирующего поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
| |
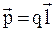
| 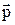 - электрический момент диполя: - электрический момент диполя: 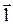 - плечо диполя. - плечо диполя.
|
s= 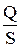
| s - поверхностная плотность заряда равна заряду, приходящемуся на единицу площади поверхности несущего заряд тела. |
r= 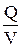
| r - объемная плотность заряда равна заряду, приходящемуся на единицу объема заряженного по объему тела. |
Е= 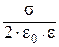
| Е - напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью: s - поверхностная плотность заряда, e0 - электрическая постоянная, e - диэлектрическая проницаемость среды нахождения плоскости. |
Е= 
| Е - напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями, в пространстве между этими плоскостями. |
WП= 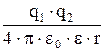
| WП - потенциальная энергия взаимодействия двух точечных зарядов, находящихся на расстоянии r друг от друга. |
j= 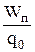
| j - потенциал электростатического поля равен потенциальной энергии единичного положительного заряда, помещенного в данную точку. |
j = 
| j - потенциал поля равен работе перемещения единичного положительного заряда из данной точки в бесконечность. |
j= 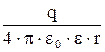
| j - потенциал поля точечного заряда на расстоянии r от него. |
| j=Sj i | принцип суперпозиции для потенциала: если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов в данной точке. |
j1- j2 = 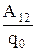 U = j1 - j2
U = j1 - j2
| разность потенциалов между двумя точками равна работе поля по перемещению единичного положительного заряда из начальной точки в конечную; U - напряжение. |
e= 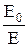
| диэлектрическая проницаемость e показывает во сколько раз электрическое поле ослабляется диэлектриком; Е0 - напряженность поля в вакууме, Е - напряженность поля в диэлектрике. | |
 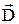 - электрическое смещение. - электрическое смещение.
| ||
Е= - 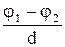 Е=
Е= 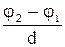
| связь между напряженностью Е и разностью потенциалов j1 - j2 для однородного электростатического поля: d - расстояние между точками поля, отсчитанное вдоль силовой линии (знак минус ² -² в первом уравнении указывает на то, что вектор напряженности поля направлен в сторону убывания потенциала). | |
Е= 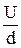
| Е – напряженность однородного электрического поля в пространстве между обкладками плоского конденсатора; U - напряжение и d – расстояние между обкладками. |
С= 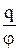
| С - электроемкость уединенного проводника равна заряду, сообщение которого проводнику изменяет его потенциал на единицу. |
С= 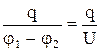
| С - электроемкость конденсатора равна отношению заряда q, накопленного в конденсаторе, к разности потенциалов (напряжению) между его обкладками. |
С= 
| С - электроемкость плоского конденсатора: S - площадь каждой из обкладок, d - расстояние между обкладками. |
| С=4 . p . e . e0 . R | С - электроемкость шара радиуса R. |
| С=SC i | С - электроемкость батареи конденсаторов при их параллельном соединении, C i – электроемкость отдельного конденсатора. |
| U=Ui | напряжения на конденсаторах при их параллельном соединении одинаковы. |
| q=Sqi | q – общий заряд на батарее конденсаторов при их параллельном соединении, qi – заряд на отдельном конденсаторе. |
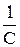 =S =S 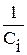
| С - электроемкость батареи конденсаторов при их последовательном соединении, C i – электроемкость отдельного конденсатора. |
| U=SUi | U – общее напряжение на батарее конденсаторов при их последовательном соединении, Ui – напряжение на отдельном конденсаторе. |
| q=qi | заряды на конденсаторах при их последовательном соединении одинаковы. |
W= 
| W - энергия заряженного конденсатора: q - заряд, U - напряжение (разность потенциалов), С - электроемкость конденсатора. |
w= 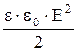
| w - объемная плотность энергии электростатического поля, Е - напряженность поля. |

| F - сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора. |
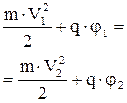
| закон сохранения энергии при движении заряженной частицы с зарядом q и массой m: V1 и V2 - скорости частицы в точках 1 и 2, j1 и j2 - потенциалы в точках 1 и 2, соответственно. |
I=  I=
I= 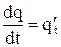
| сила тока I равна заряду, протекающему через поперечное сечение проводника в единицу времени. |
j= 
| плотность тока j равна силе тока, протекающего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока. |
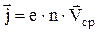
| направление вектора плотности тока 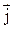 совпадает с направлением упорядоченного движения положительных зарядов, n - концентрация носителей тока, совпадает с направлением упорядоченного движения положительных зарядов, n - концентрация носителей тока, 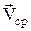 - скорость упорядоченного движения зарядов в проводнике (скорость дрейфа), е - заряд носителей тока. - скорость упорядоченного движения зарядов в проводнике (скорость дрейфа), е - заряд носителей тока.
|
I= 
| закон Ома для (однородного) участка цепи: I - сила тока, U - напряжение на участке цепи равно разности потенциалов, т.е. U = j1 - j2, R - сопротивление участка цепи. |
R= 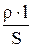
| R - сопротивление однородного линейного проводника длиной l с постоянной площадью поперечного сечения S, r - удельное электрическое сопротивление проводника. |
s= 
| s - удельная электрическая проводимость вещества, r - удельное электрическое сопротивление. |
r=r0(1+at)
a= 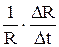
| зависимость удельного сопротивления r от температуры: r0 - удельное сопротивление при 0 °С, a - температурный коэффициент сопротивления равен относительному изменению сопротивления при нагреве на 1 °С (1 К). | |
| R=SRi | R - общее сопротивление цепи при последовательном соединении проводников, Ri- сопротивление i-го проводника. | |
| U=SUi | U – общее напряжение в цепи последовательно соединенных проводников; Ui – напряжение на сопротивлении Ri. | |
| I=Ii | сила тока в цепи последовательно соединенных сопротивлений одинакова на всех проводниках. | |

| R - общее сопротивление цепи при параллельном соединении проводников, Ri - сопротивление i-го проводника. |
| U=Ui | напряжение при параллельном соединении проводников одинакова на всех сопротивлениях |
| I=SIi | I – общая сила тока при параллельном соединении проводников; Ii – сила тока на сопротивлении Ri. |
U= 
| напряжение U равно работе электрического поля по перемещению единичного электрического заряда на данном участке цепи. |
Е= 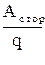
| Е - электродвижущая сила (ЭДС), действующая в цепи, равна работе сторонних сил по перемещению единичного положительного заряда. |
I= 
| закон Ома для замкнутой (полной) цепи: сила тока I в замкнутой цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме внешнего R и внутреннего r сопротивлений. |
I= 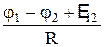 U = IR =
=j1-j2 + Е 12
U = IR =
=j1-j2 + Е 12
| закон Ома для неоднородного участка цепи (участка цепи с источником тока): j1 - j2 - разность потенциалов на концах участка цепи, Е 12 - ЭДС источника (источников) тока, входящего в участок с сопротивлением R. U - напряжение на неоднородном участке цепи не равно разности потенциалов, т.е. U 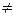 j1 - j2. j1 - j2.
|
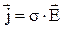 = = 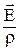
| закон Ома в дифференциальной форме: j - плотность тока, s - удельная электропроводность, r - удельное сопротивление, Е - напряженность электростатического поля. |
| SIK=0 | первое правило Кирхгофа: алгебраическая сумма сил токов, сходящихся в узле, равна нулю. |
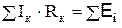
| второе правило Кирхгофа: для любого замкнутого контура разветвленной электрической цепи алгебраическая сумма произведений сил токов Iк на сопротивления Rк соответствующих участков этого контура равна алгебраической сумме ЭДС Еi в этом контуре. |
I= 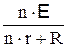
| закон Ома для замкнутой цепи при последовательном соединении n одинаковых источников тока: n - число источников тока, r - внутреннее сопротивление каждого из источников, Е - ЭДС отдельного источника, R - внешнее сопротивление цепи. |
I= 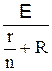
| закон Ома для замкнут |
|
|
