Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вынужденные электрические колебания

Для получения в реальном контуре незатухающих колебаний нужно компенсировать потери энергии электромагнитного поля, связанные с ее переходом в теплоту, подключив контур к источнику внешней переменной ЭДС. Считая токи в контуре квазистационарными, будем применять к мгновенным значениям всех электрических величин законы постоянного тока (переменные токи можно считать квазистационарными, если время t, в течение которого электрические величины принимают установившиеся значения, мало по сравнению с периодом колебаний Т, т.е. должно быть t< < Т). Будем предполагать, что колебания в контуре являются установившимися, т.е. с момента начала колебаний прошло достаточно продолжительное время, так что амплитуды заряда, тока и напряжения достигли постоянного значения. В этом случае имеем вынужденные электромагнитные колебания в контуре с частотой внешнего источника. Рассмотрим последовательно процессы, происходящие в цепи, содержащей резистор, катушку индуктивности и конденсатор, если в цепи имеется переменный ток, сила которого изменяется по синусоидальному закону

I(t) = I₀sinwt. (47.1)

1. Сопротивление R в цепи переменного тока (рисунок 59). Применяя к рассматриваемому участку цепи закон Ома, имеем:

U_R = IR = I₀Rsinwt = U₀sinwt, (47.2)

где U₀ = I₀R – амплитудное значение напряжения.

Для наглядного изображения соотношений между током и напряжением воспользуемся методом векторных диаграмм. Так как разность фаз между током I и напряжением U_R на резисторе равна нулю, то вектор направим вдоль оси тока (см. рисунок 59).

2. Емкость С в цепи переменного тока (рисунок 60). Напряжение U_C на конденсаторе равно U_C = q /C, где

q = .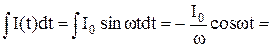

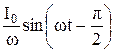Следовательно,

U_C = 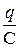= = 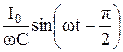U₀ 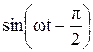, (47.3)

где

U₀ = I₀ 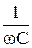(47.4)

– амплитудное значение напряжения. Сравнивая выражения (47.1) и (47.3) видим, что колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2. Это показано на векторной диаграмме (см. рисунок 60).

Сравнивая выражение (47.4) с законом Ома для участка цепи, видим, что величина

Х_С = 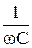(47.5)

играет роль сопротивления участка цепи, и ее называют (реактивным) емкостным сопротивлением. Как видно из (47.5) емкостное сопротивление Х_С зависит от частоты w. В частности, для постоянного тока (w = 0) Х_С ® ¥, а для очень больших частот (w ® ¥) Х_С ® 0.

3. Индуктивность L в цепи переменного тока (рисунок 61). Если бы сопротивление катушки индуктивности было равно R, то закон Ома для неоднородного участка цепи записывается так:

U_L = IR - E.

На схеме R = 0, а ЭДС самоиндукции равна

E = - LI¢.

Тогда

U_L = LI¢ = L(I₀sinwt)¢ = I₀wLcoswt = U₀ 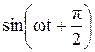, (47.6)

где

U₀ = I₀wL (47.7)

– амплитудное значение напряжения. Сравнивая выражения (47.1) и (47.6) видим, что колебания напряжения на катушке индуктивности опережают по фазе колебаний тока на p/2. Это показано на векторной диаграмме (см. рисунок 59).

Сравнивая выражение (47.7) с законом Ома для участка цепи, видим, что величина

Х_L = wL (47.8)

играет роль сопротивления участка цепи, и ее называют (реактивным) индуктивным сопротивлением. Как видно из (47.8) индуктивное сопротивление Х_L прямо пропорционально частоте w. Поэтому для постоянного тока (w = 0) Х_L = 0, а для очень больших частот (w ® ¥) Х_L ® ¥.

3. Закон Ома для цепи переменного тока. Рассмотрим цепь переменного тока, состоящую из последовательно соединенных сопротивления R, емкости С и катушки индуктивности L (см. рисунок 62). В цепи протекает переменный ток, вызывающий на R, L, C соответствующие падения напряжения U_R, U_L, U_C. Для получения амплитуды результирующего напряжения на входе цепи воспользуемся векторной диаграммой напряжений, используя результаты, изложенные ранее. На векторной диаграмме (см. рисунок 62) отложены амплитуды падений напряжений на резисторе U_R, катушке индуктивности U_L, емкости U_C.

Складывая U_L и U_C, получим одно гармоническое колебание, изображаемое вектором 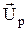, имеющим модуль

U_p = U_L - U_C = I₀ 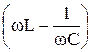= I₀(X_L - X_C) = I₀X, (47.9)

где Х – называют реактивным сопротивлением цепи.

X_L и X_C - называют реактивными сопротивлениями потому, что в отличие от активного сопротивления R, на X_L и X_C не выделяется джоулево тепло, которое, как известно, Q = I²Rt.

Полное напряжение U₀ на входе цепи равно

U₀ = = =

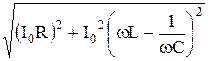= I₀ 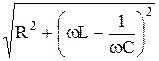= I₀ Z, (47.10)

где Z – называют полным сопротивлением цепи переменного тока или импедансом, U_p – называют реактивной составляющей напряжения, U_R – активной составляющей напряжения.

Складывая U_p и U_R. получаем гармонические колебания напряжения на входе:

U(t) = U₀sin(wt + j), (47.11)

где j - сдвиг по фазе между напряжением и током (см. (47.1) и (47.11)).

Напряжение U(t) на входе цепи равно ЭДС генератора Е(t).

Из векторной диаграммы (рисунок 62) видно, что

tgj = 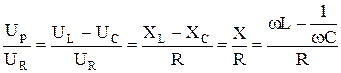, (47.12)

и

cosj = 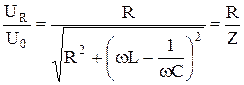. (47.13)

Величину cosj при вычислении мощности в цепи переменного тока называют коэффициентом мощности. Записанные выше уравнения (47.10) и (47.12) выражают закон Ома для цепи переменного тока.

Уравнение (47.10), выражающее закон Ома для цепи переменного тока, можно выразить как функциональную зависимость силы тока I от частоты w:

I₀(w) = 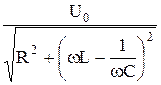. (47.14)

Функция I₀(w) достигает максимального значения, равного 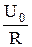, при условии 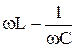= 0, из которого находим значение частоты w = w₀ = 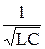, соответствующей максимуму функции I₀(w). При совпадении частот вынужденных (w) и собственных (w₀) электромагнитных колебаний, т.е. при w = w₀, в колебательном контуре наблюдают явление электрического резонанса. В случае резонанса напряжения на конденсаторе U_C и катушке индуктивности U_L противоположны по фазе и равны по амплитуде:

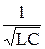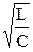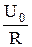
(U_L)_рез = (U_C)_рез = I₀w₀L = I₀ L = I₀ = = 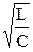U₀Q, (47.15)

где Q = 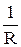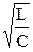- добротность колебательного контура.

Поскольку добротность обычных колебательных контуров Q > 1, то согласно соотношению (47.15) амплитуды напряжений (U_L)_рез и (U_C)_рез больше амплитуды напряжения U₀ на входе цепи в Q раз.

Таким образом, при резонансной частоте w = w₀ амплитуда тока достигает максимального значения, а разность фаз между током и напряжением становится равной нулю 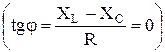, т.е. контур для переменного тока представляет чисто активное сопротивление R. При рассмотренном случае резонанса, который называют резонансом напряжений, напряжения на катушке индуктивности (U_L)_рез и конденсаторе (U_C)_рез, равные по модулю, в Q раз превышают напряжение U₀ на входе цепи. Поэтому явление резонанса напряжений используют в технике радиосвязи для усиления колебаний напряжения какой-либо определенной частоты (из многих сигналов различных частот). В радиосхемах усиленное напряжение обычно снимают с конденсатора или катушки индуктивности.

Так как при резонансе напряжений в колебательном контуре напряжения (U_L)_рез на индуктивности и (U_C)_рез на емкости в Q раз больше, чем входное напряжение, то при большой добротности Q колебательного контура может произойти пробой. Поэтому явление резонанса напряжений необходимо учитывать при расчете изоляции колебательных контуров.

Когда говорят, что в цепи отсутствует емкость (индуктивность), это нужно понимать как X_C = 0 (X_L = 0).

Хотя реактивное сопротивление измеряют в тех же единицах, что и активное (т.е. в Омах), между ними существует принципиальное различие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту.