Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Свободные затухающие колебания

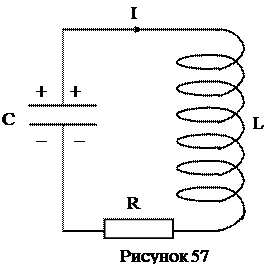
В § 9.45 мы предполагали, что электрическое сопротивление катушки, включенной в контур, равно нулю. Создать идеальный колебательный контур на практике не удается, так как и катушка индуктивности и соединительные провода имеют отличное от нуля активное (омическое) сопротивление R (через R обозначим их суммарное сопротивление). Таким образом, в реальном колебательном контуре (см. рисунок 57) наряду с процессом перехода энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно происходит выделение тепла Джоуля-Ленца на сопротивлении R. Электромагнитные колебания в реальном контуре описываются уравнением (45.1):

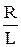q ¢ ¢ + q ¢ + 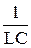q = 0. (46.1)

Вводя обозначения

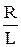= 2b, 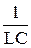= w₀², (46.2)

перепишем уравнение (46.1)

q ¢ ¢ + 2b q ¢ +w₀² q = 0. (46.3)

В уравнении (46.3) величину w₀ называют собственной частотой контура, b - коэффициентом затухания. Так как в схеме, приведенной на рисунке 57, внешние переменные ЭДС Е отсутствуют, а R ¹ 0, то уравнение (46.3) описывает свободные затухающие колебания (колебательная система, в которой происходят затухающие колебания, называется диссипативной). При b < w₀ решение этого однородного дифференциального уравнения второго порядка имеет вид:

q (t) = q ₀ cos(wt + a), (46.4)

где w = 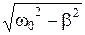= , (46.5)

q ₀ и a - постоянные, определяемые из начальных условий, а величина

А = q ₀ 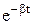(46.6)

- амплитуда затухающих колебаний.

Зависимость (46.4) показана на рисунке 58 сплошной линией, а зависимость (46.6) - штриховыми линиями. Затухающие колебания не имеют определенного значения периода колебаний. Но при малом затухании небольшие интервалы зависимости q (t) можно принять за отрезки соответствующей синусоиды и считать затухающие колебания как гармонические колебания, амплитуда которых непрерывно уменьшается с течением времени по закону q ₀ 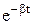. В этом случае условный период затухающих колебаний равен:

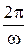Т = = . (46.7)

С увеличением сопротивления контура R частота w уменьшается, а период колебаний Т увеличивается. Через время Т достигаются максимальные и минимальные значения заряда (а также силы тока и напряжения).

Разделив функцию (46.4) на емкость С, получим напряжение на конденсаторе:

U(t) = 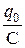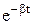cos(wt + a) = U₀ 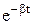cos(wt + a), (46.8)

Чтобы найти силу тока, продифференцируем (46.4) по времени

I(t)= q ¢ = q ₀ 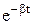[- bcos(wt + a) - wsin(wt + a)].

Преобразуем выражение в квадратных скобках к косинусу. Для этого умножим и разделим это выражение на w₀ (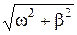 = w₀), а затем введем угол d по формулам

-b/w₀ = cosd, w/w₀ = sind. (46.9)

После этого выражение для силы тока примет вид

I(t)= w q ₀ 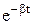cos(wt + a + d). (46.10)

Из (46.9) следует, что угол d лежит во второй четверти (p/2 < d < p). Это означает, что при наличии активного сопротивления R ток в контуре опережает по фазе напряжение (46.8) на конденсаторе более чем на p/2 (при R=0 опережение составляет d = p/2).

Графики зависимостей U(t)иI(t) имеют вид, аналогичный зависимости q (t) (см. рисунок 58).

Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации (е» 2, 72). Из формулы (46.4) легко определить, что

t = 1/b. (46.11)

Затухание колебаний принято характеризовать логарифмическим декрементом затухания. Он определяется как натуральный логарифм отношения двух значений амплитуд заряда (или тока, напряжения), взятых через период колебания Т:

l = 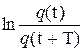= bТ = 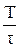= , (46.12)

где l - логарифмический декремент затухания; N_e - число колебаний, совершаемых за время уменьшения амплитуды в е раз.

Логарифмический декремент затухания - постоянная для данной колебательной системы величина.

Если затухание мало (b < < w₀), то w» w₀ = 1/ 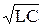и согласно (46.12)

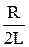
l» b× = = = 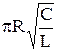. (46.13)

Для характеристики затухания контуров вводят понятие добротности колебательного контура Q, пропорциональной отношению энергии, запасенной в контуре, к ее изменению DW за период Т:

Q = 2p 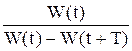. (46.14)

Энергия, равная DW = W(t) - W(t + T), рассеивается на сопротивлении R за время Т в виде теплоты Джоуля-Ленца. В реальных контурах значение добротности лежит в интервале 50 – 200. Добротность также равна

Q = = p N_e, (46.15)

где l - логарифмический декремент затухания.

Из формулы (46.15) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации. Чем меньше затухание, тем больше Q. При слабом затухании (b < < w₀) согласно (46.13) добротность равна

Q = . (46.16)

В заключение отметим, что при увеличении коэффициента затухания b период затухающих колебаний растет, и при b ³ w₀ вместо колебаний происходит апериодический разряд конденсатора. Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления R_кр определяется из условия b = w₀ и, подставляя значения b и w₀ из (46.2), имеем

R_кр = . (46.17)

Для получения длительно существующих электрических (также и механических) колебаний большое значение имеют так называемые автоколебательные системы. Автоколебательные системы реальные устройства, сопротивление которых не равно нулю.

В автоколебательных системах незатухающие колебания возникают под влиянием процессов, происходящих внутри системы, и для их поддержания не требуется никаких внешних воздействий. В состав автоколебательной системы входит источник энергии (в случае механических колебаний – сжатая пружина, поднятый груз и т.д., в случае электрических колебаний – источник тока). Этот источник периодически включается самой системой и вводит в нее определенную энергию, компенсирующую потери на выделение тепла Джоуля-Ленца, что и делает колебания незатухающими.