
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Колебательный контур
|
|
Неразрывная связь между электрическими и магнитными явлениями заключается в том, что любое изменение электрического поля порождает вихревое магнитное поле, а любое изменение магнитного поля приводит в свою очередь к появлению вихревого электрического поля. По этой причине электрические и магнитные колебания могут существовать только совместно, и такие колебания называют электромагнитными колебаниями. При электромагнитных колебаниях периодически изменяющимися величинами являются параметры электрического и магнитного полей.
Для возбуждения и поддерживания электромагнитных колебаний используют колебательный контур – цепь, состоящую из последовательно включенных катушки индуктивностью L и конденсатора емкостью С (см. рисунок 54). Электромагнитные колебания, происходящие в колебательном контуре за счет первоначально сообщенной этому контуру энергии, которая в дальнейшем не пополняется, называют свободными (собственными) электромагнитными колебаниями. Собственные электромагнитные колебания происходят под действием процессов, происходящих в самом колебательном контуре. Если пренебречь сопротивлением проводов катушки индуктивности (R» 0), то можно пренебречь потерями на выделение тепла Джоуля-Ленца. Если к тому же не учитывать незначительные потери энергии на излучение электромагнитных волн в окружающее пространство, то мы имеем незатухающие электромагнитные колебания в контуре.
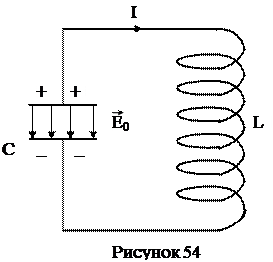 Рассмотрим превращения энергии в колебательном контуре при свободных незатухающих электромагнитных колебаниях. Предположим, что, разомкнув контур, зарядили конденсатор. Между обкладками конденсатора появляется электрическое поле, которое обладает определенной энергией. Замкнем конденсатор на катушку. В этот момент времени (t = 0) напряженность электрического поля Е0 между обкладками конденсатора, напряжение U0 между обкладками и заряд q 0 на обкладках конденсатора максимальны. Тока в контуре еще нет, следовательно, отсутствует и магнитное поле. При этом вся энергия W колебательного контура сосредоточена в виде энергии электрического поля в конденсаторе, т.е. W =
Рассмотрим превращения энергии в колебательном контуре при свободных незатухающих электромагнитных колебаниях. Предположим, что, разомкнув контур, зарядили конденсатор. Между обкладками конденсатора появляется электрическое поле, которое обладает определенной энергией. Замкнем конденсатор на катушку. В этот момент времени (t = 0) напряженность электрического поля Е0 между обкладками конденсатора, напряжение U0 между обкладками и заряд q 0 на обкладках конденсатора максимальны. Тока в контуре еще нет, следовательно, отсутствует и магнитное поле. При этом вся энергия W колебательного контура сосредоточена в виде энергии электрического поля в конденсаторе, т.е. W = 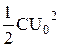 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Когда конденсатор начинает разряжаться, напряжение на нем и напряженность электрического поля между обкладками будут уменьшаться. Из-за возникшего в контуре электрического тока разряда конденсатора в катушке индуктивности появится магнитное поле. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая мгновенному нарастанию этого тока. Через время, равное четверти периода колебаний (t = 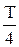 ) конденсатор полностью разряжается (U = 0; E = 0), а сила тока I0 в контуре и индукция магнитного поля В0 этого тока достигают максимальных значений. В этот момент времени вся энергия контура заключена в виде энергии магнитного поля в катушке индуктивности, т.е. W =
) конденсатор полностью разряжается (U = 0; E = 0), а сила тока I0 в контуре и индукция магнитного поля В0 этого тока достигают максимальных значений. В этот момент времени вся энергия контура заключена в виде энергии магнитного поля в катушке индуктивности, т.е. W = 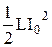 .
.
В интервале времени от 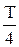 до
до 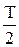 магнитное поле будет уменьшаться. Уменьшающееся магнитное поле вызывает экстраток самоиндукции, который в соответствии с правилом Ленца стремится поддержать ток разряда конденсатора и будет направлен так же, как и ток разряда. Конденсатор начинает перезаряжаться и между его обкладками появится электрическое поле противоположного направления. Это поле стремится ослабить ток, который в момент времени t =
магнитное поле будет уменьшаться. Уменьшающееся магнитное поле вызывает экстраток самоиндукции, который в соответствии с правилом Ленца стремится поддержать ток разряда конденсатора и будет направлен так же, как и ток разряда. Конденсатор начинает перезаряжаться и между его обкладками появится электрическое поле противоположного направления. Это поле стремится ослабить ток, который в момент времени t = 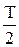 обратится в нуль, а заряд q 0 на обкладках конденсатора (соответственно, напряженность электрического поля Е0 и напряжение U0) достигает первоначального максимального значения.
обратится в нуль, а заряд q 0 на обкладках конденсатора (соответственно, напряженность электрического поля Е0 и напряжение U0) достигает первоначального максимального значения.
В интервале времени от 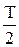 до
до 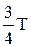 конденсатор будет снова разряжаться. При этом в контуре возникает ток, направленный противоположно току в предыдущей стадии процесса. В момент времени t =
конденсатор будет снова разряжаться. При этом в контуре возникает ток, направленный противоположно току в предыдущей стадии процесса. В момент времени t = 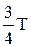 конденсатор полностью разряжается, т.е. напряжение U между его обкладками становится равным нулю (соответственно, q = 0 и Е = 0), а ток I0 и индукция В0 магнитного поля достигают максимальных значений. В этот момент вся энергия электрического поля снова превращается в энергию магнитного поля.
конденсатор полностью разряжается, т.е. напряжение U между его обкладками становится равным нулю (соответственно, q = 0 и Е = 0), а ток I0 и индукция В0 магнитного поля достигают максимальных значений. В этот момент вся энергия электрического поля снова превращается в энергию магнитного поля.
В интервале времени от 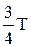 до Т возникшая в катушке индуктивности ЭДС самоиндукции поддерживает убывающий ток и перезаряжает конденсатор, и через промежуток времени, равный периоду колебаний (t = Т), электрическое состояние контура будет таким же, как и в момент t = 0.
до Т возникшая в катушке индуктивности ЭДС самоиндукции поддерживает убывающий ток и перезаряжает конденсатор, и через промежуток времени, равный периоду колебаний (t = Т), электрическое состояние контура будет таким же, как и в момент t = 0.
После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. При отсутствии энергетических потерь процесс взаимных периодических превращений энергий электрического поля и магнитного поля будет продолжаться неограниченно долго, и мы получим незатухающие электромагнитные колебания. При этом в контуре периодически изменяются (колеблются) заряд q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Для получения уравнения колебаний заряда q в контуре вначале положим, что контур обладает активным сопротивлением R. Тогда согласно закону Ома
UR + UC = E,
где UR = IR – напряжение на сопротивлении,
UC = 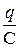 - напряжение на конденсаторе,
- напряжение на конденсаторе,
E = - L 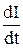 = - LIt¢ = - L q ¢ ¢ tt, (I = q ¢ t, It¢ = q ¢ ¢ tt),
= - LIt¢ = - L q ¢ ¢ tt, (I = q ¢ t, It¢ = q ¢ ¢ tt),
Е – ЭДС самоиндукции, возникающая в катушке.
Итак,
IR + 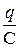 = - L q ¢ ¢,
= - L q ¢ ¢,
откуда, поделив все слагаемые на L, имеем:
q ¢ ¢ + 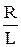 q ¢ +
q ¢ + 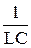 q = 0. (45.1)
q = 0. (45.1)
Поскольку в колебательном контуре внешние ЭДС отсутствуют, то рассмотренные электромагнитные колебания представляют собой свободные колебания. Если сопротивление контура R = 0, то уравнение (45.1) примет вид:
q ¢ ¢ + 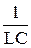 q = 0. (45.2)
q = 0. (45.2)
или, обозначая w0 = 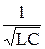 , получим
, получим
q ¢ ¢ + w02q = 0. (45.3)
Уравнение (45.3) представляет собой дифференциальное уравнение свободных гармонических колебаний заряда в контуре, которое, как легко проверить подстановкой, имеет решение:
q (t) = q 0cos(w0t + a), (45.4)
где q 0 – амплитуда колебаний заряда на обкладках конденсатора, w0 - циклическая частота колебаний (собственная частота контура), a - начальная фаза.
Период свободных колебаний в идеальном контуре (т.е. при R = 0) равен:
Т = 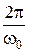 = 2p
= 2p 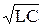 . (45.5)
. (45.5)
Формула (45.5) впервые была получена У. Томсоном и называется формулой Томсона. Частота колебаний
n = 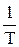 =
= 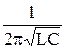 . (45.6)
. (45.6)
В выражении (45.4) значения амплитуды колебаний заряда q 0 и начальной фазы a определяют из начальных условий, т.е. значениями силы тока I(0) и заряда q (0) (или напряжения U(0) = q (0)/С) в момент времени t = 0.
Напряжение на обкладках конденсатора равно:
UC = U(t) =  q (t) =
q (t) = 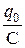 cos(w0t + a) = U0cos(w0t + a), (45.7)
cos(w0t + a) = U0cos(w0t + a), (45.7)
где U0 = 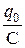 - амплитуда колебаний напряжения на конденсаторе.
- амплитуда колебаний напряжения на конденсаторе.
Сравнивая выражения (45.4) (45.7) убеждаемся, что заряд q (t) и напряжение U(t) колеблются в фазе друг с другом.
Сила тока в колебательном контуре равна:
I(t) = I = q ¢ t = - w0 q 0sin(w0t + a) = I0cos(w0t + a + 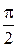 ), (45.8)
), (45.8)
где I0 = w0 q 0, - амплитуда силы тока.
Сопоставляя выражения (45.4) и (45.8) заключаем, что колебания тока опережает по фазе колебания заряда на 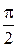 , т.е. когда ток достигает максимального значения, заряд равен нулю, и наоборот.
, т.е. когда ток достигает максимального значения, заряд равен нулю, и наоборот.
Уравнения (45.4), (45.7), (45.8) для a = 0 записываются так:
q (t) = q 0cosw0t, UC(t) = U0cosw0t, I(t) = I0cos(w0t + 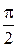 ),
),
 и графики этих зависимостей q (t), UC(t), I(t) представлены на рисунке 55.
и графики этих зависимостей q (t), UC(t), I(t) представлены на рисунке 55.
Если в формуле Томсона Т = 2p 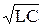 индуктивность измерять в генри ([L] = Гн), емкость в фарадах ([С] = Ф), то период колебаний будет измеряться в секундах ([Т] = с).
индуктивность измерять в генри ([L] = Гн), емкость в фарадах ([С] = Ф), то период колебаний будет измеряться в секундах ([Т] = с).
Из закона сохранения энергии следует, что в идеальном контуре (R = 0) максимальные значения энергии электрического и магнитного полей равны, т.е.
 , (45.9)
, (45.9)
откуда с учетом того, что I0 = w0 q 0, опять приходим к результату
w02 = 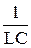 . (45.10)
. (45.10)
Для произвольного момента времени энергии электрического поля и магнитного поля равны, соответственно:
Wэл(t) = 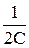 q 2(t) =
q 2(t) = 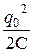 cos2(w0t + a) =
cos2(w0t + a) = 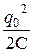
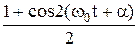 =
=
= 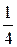
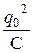 (1 + cos(2w0t + 2a)), (45.11)
(1 + cos(2w0t + 2a)), (45.11)
Wм(t) = 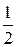 LI2(t) =
LI2(t) = 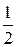 LI02sin2(w0t + a) =
LI02sin2(w0t + a) = 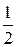 LI02
LI02 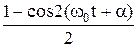 =
=
= 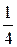 LI02 (1 -cos(2w0t + 2a)). (45.12)
LI02 (1 -cos(2w0t + 2a)). (45.12)
Из уравнений (45.11) и (45.12) следует, что энергии электрического поля и магнитного поля в контуре изменяются с частотой, в два раза превышающей частоту гармонических электрических колебаний (заряда, силы тока, напряжения) в контуре.
Полная энергия W контура складывается из энергий электрического и магнитного полей и равна максимальному значению энергии электрического или магнитного поля:
W = Wэл(t) + Wм(t) =  . (45.13)
. (45.13)
Полная энергия W остается постоянной, т. е. неизменной со временем.
Уравнения колебаний энергий электрического поля Wэл(t) и магнитного поля Wм(t), т.е. выражения (45.11) и (45.12), для a=0 с учетом соотношения (45.13) для полной энергии W принимают вид:
Wэл(t) = 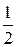 W× (1 + cos2w0t), Wм(t) =
W× (1 + cos2w0t), Wм(t) = 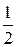 W× (1 - cos2w0t),
W× (1 - cos2w0t),
и графики этих зависимостей Wэл(t) и Wм(t) представлены на рисунке 56.
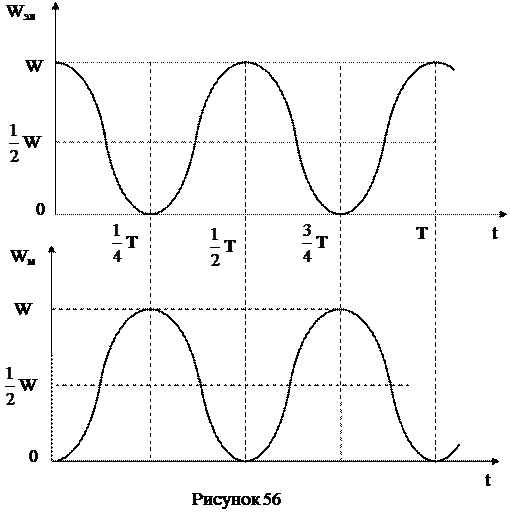
Как видно из графиков энергии Wэл(t) и Wм(t) совершают гармонические колебания в противофазе по отношению друг другу около равновесного положения 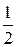 W ( W – полная энергия контура) с частотой в два раза превышающей частоту гармонических колебаний в контуре.
W ( W – полная энергия контура) с частотой в два раза превышающей частоту гармонических колебаний в контуре.
|
|
