
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения Максвелла для электромагнитного поля
|
|
В теории Максвелла мысль о тесной связи электрических и магнитных явлений получила окончательное оформление в виде двух основных положений, рассмотренных нами в предыдущих параграфах. Эта теория позволила с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения.
1. Электрическое поле (см. § 8.40) может быть как потенциальным (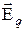 ), так и вихревым (
), так и вихревым (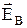 ), поэтому напряженность суммарного поля равна их сумме
), поэтому напряженность суммарного поля равна их сумме 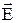 =
= 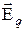 +
+ 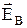 . Так как циркуляция вектора
. Так как циркуляция вектора 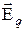 равна нулю (см. (40.3)), а циркуляция вектора
равна нулю (см. (40.3)), а циркуляция вектора 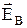 определяется выражением (40.2), то циркуляция вектора напряженности суммарного поля (
определяется выражением (40.2), то циркуляция вектора напряженности суммарного поля (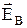 и
и 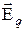 ) равна
) равна
 = -
= - 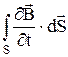 . (42.1)
. (42.1)
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора 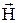 (см. (41.7)):
(см. (41.7)):
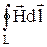 =
=  . (42.2)
. (42.2)
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Остроградского - Гаусса для электрического поля (см. (9.4)):
 =
= 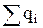 . (42.3)
. (42.3)
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (42.3) запишется в виде
 =
=  . (42.4)
. (42.4)
4. Теорема Остроградского - Гаусса для магнитного поля (см. (25.3)):
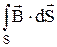 = 0. (42.5)
= 0. (42.5)
Итак, полная система уравнений Максвелла в интегральной форме:
 = -
= - 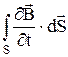 ;
;  =
=  ;
;
(42.6)
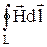 =
=  ;
; 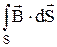 = 0.
= 0.
Величины, входящие в уравнения Максвелла, не являются независимыми. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов.
Для изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков, в случае достаточно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени между ними существует следующая связь:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
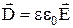 ;
; 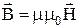 ;
; 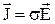 , (42.7)
, (42.7)
где e0 и m0 - электрическая и магнитная постоянные, соответственно; e и m - диэлектрическая и магнитная проницаемости, соответственно; s - удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет магнитных зарядов.
Для стационарных полей (Е = const и В = const) уравнения Максвелла примут вид
 = 0;
= 0;  = q;
= q;
(42.8)
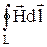 = I;
= I; 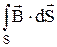 = 0.
= 0.
Т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного - только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
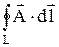 =
= 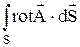 и
и  =
= 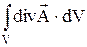
можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):
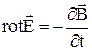 ;
; 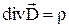 ;
;
(42.9)
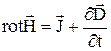 ;
; 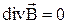 .
.
Если заряды и токи распределены в пространстве непрерывно, то обе формы записи уравнений Максвелла - интегральная и дифференциальная - эквивалентны. Однако когда имеются поверхности разрыва - поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены ранее (см. § 2.10 и § 7.37):
D1n = D2n; Е1t = Е2t; В1n = В2n ; Н1t = Н2t. (42.10)
Первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Уравнения Максвелла содержат в себе все основные законы электрического и магнитного полей, включая электромагнитную индукцию, и поэтому являются наиболее общими уравнениями для электромагнитного поля в покоящихся средах. Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно - без электрических зарядов и токов. При этом переменное магнитное поле всегда связано с порождаемым им электрическим полем, и обратно, переменное электрическое поле всегда связано с порождаемым им магнитным полем. Одним из важных выводов теории Максвелла явилось существование магнитного поля токов смещения (§ 8.41), что позволило Максвеллу предсказать существование электромагнитных волн - переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. Таким образом, электрическое и магнитное поля неразрывно связаны друг с другом, - они образуют единое электромагнитное поле, распространяющееся в пространстве – электромагнитные волны.
Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила установить их общие свойства:
- скорость распространения в непроводящей нейтральной неферромагнитной среде v = c / 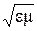 , с = 1/
, с = 1/ 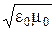 , где с – скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме (она равна скорости света в вакууме с = 3× 108 м/с;
, где с – скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме (она равна скорости света в вакууме с = 3× 108 м/с;
- векторы 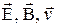 - образуют взаимно перпендикулярную правовинтовую систему;
- образуют взаимно перпендикулярную правовинтовую систему;
- в электромагнитной волне векторы 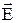 и
и  колеблются в одинаковых фазах.
колеблются в одинаковых фазах.
Максвелл также показал, что электромагнитное поле обладает энергией и импульсом. Электромагнитные волны, отражаясь или поглощаясь в телах, на которые они падают, оказывают на них давление.
Максвелл блестяще развил электромагнитную теорию света. Свет представляет собой электромагнитные волны определенного диапазона частот.
Максвелл предсказал, что колебания заряда в резонансном контуре приведут к испусканию электромагнитных волн, т.е. Максвелл предсказал возможность радиосвязи задолго до открытия радиоволн.
Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857-1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла получила полное блестящее экспериментальное подтверждение.
Контрольные вопросы
1 Что является причиной возникновения вихревого электрического поля? Чем оно отличается от электростатического поля?
2 Чему равна циркуляция вихревого электрического поля?
3 Почему вводится понятие тока смещения? Что он собой по существу представляет?
4 Выведите и объясните выражение для плотности тока смещения.
5 В каком смысле можно сравнивать ток смещения и ток проводимости?
6 Запишите, объяснив физический смысл, обобщенную теорему о циркуляции вектора напряженности магнитного поля.
7 Запишите полную систему уравнений Максвелла в интегральной и дифференциальной формах и объясните их физический смысл.
8 Почему постоянные электрические и магнитные поля можно рассматривать обособленно друг от друга? Запишите для них уравнение Максвелла в обеих формах.
9 Почему уравнения Максвелла в интегральной форме являются более общими?
10 Какие основные выводы можно сделать на основе теории Максвелла?
|
|
