Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Постановка задачи .

Примечание:

1. Учитывая, как правило, большие высоты полета на пассивном участке, аэродинамические силы сопротивления не учитываем.

2. По той же причине будем учитывать изменение силы тяжести.

3. 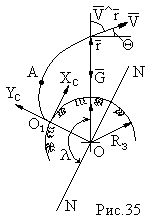В связи с большими дальностями полета поле тяготения Земли будем рассматривать центральным, т.е. учитывая кривизну Земли.

4. В пределах расчета одного витка траектории для спутника или расчета траектории ракет класса “Земля – Земля” не будем учитывать вращение Земли.

Дано: V_A, Θ _A , X_A, Y_A, m=const.

Определить: L_эл – дальность полета на эллиптическом участке траектории;

T_эл – время полета на эллиптическом участке траектории.

Запишем дифференциальное уравнение движения на эллиптическом участке в векторной форме:

где g – ускорение действующее на ракету на высоте полета.

- ускорение на уровне Земли.

Таким образом получаем:

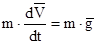
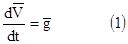- дифференциальное уравнение движения полета ракеты на пассивном участке в векторной форме.

Тогда: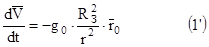

r = R_З + H, где Н – высота полета ракеты над поверхностью Земли.

Для решения уравнения (1) или (1’) необходимо получить два интеграла.