Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Требования к траектории .

1. Программа полета должна обеспечивать минимум рассеивания траектории в конце АУТ. В связи с этим угол траектории Θ в конце АУТ должен быть оптимальным. Анализ траектории показывает, что значение оптимального угла Θ может определяться:

§ С точки зрения максимальной дальности полета;

§ С точки зрения минимального рассеивания точек попадания.

Известно, что эти значения угла Θ не совпадают между собой. Будем учитывать

оптимальное значение угла Θ, полученное из условий максимальной дальности полета.

2. Как правило старт тяжелых ракет – вертикальный, а время движения на вертикальном участке невелико. Вертикальный старт объясняется:

§ Условиями устойчивости движения ракеты в начале полета;

§ Удобство старта ракеты с горизонтального стола.

3. Траектория движения ракеты на АУТ не должна иметь резких перегибов. Математически это означает, что должны быть заложены ограничения на первую и вторую производные от угла траектории Θ. Известно, что

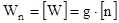- нормальное ускорение;

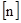- коэффициент перегрузки.

Таким образом первая производная определяет нормальное ускорение W_n и позволяет определить силу действующую на корпус ракеты при маневрах. Ограничение на вторую производную от угла Θ связаны с суммой моментов действующих на ракету относительно оси Z.

4. При выводе уравнений движения баллистических ракет предполагается, что ракета является абсолютно жестким телом, т.е. не учитывают упругость корпуса ракеты и наличие жидкости в баках.